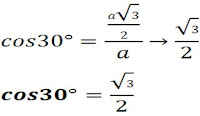A 4ª Dimensão - Matemática X Física

O que os físicos agora descobriram há muito que os matemáticos já sabiam. Do que se trata? Das inúmeras dimensões!

O mundo ao nosso redor é constituído de 3 dimensões - comprimento, largura e altura/profundidade. Pois bem a idéia que durante muito tempo se saia bizarra é que podem existir mais uma dimensão, uma quarta ao qual popularemente ficou conhecida como tempo. Seu maior expoente , o físico alemão Albert Eisntein o provou através de cálculos matemáticos, mas até que ponto  a sua descoberta tem a ver com essa relação matemática? Pode parecer meio complicado de mais de se entender, mas não é bem assim quanto se pensa não!

Figura 1: Hipercubo - Tentativa gráfica 4D

Uma função de várias variávies como f(x, y, t, z, ...n), pode assumir quatro ou mais variáveis, que aqui denominamos de x, y, t, z  e mais outras que se queira colocar, n. Até f(x,y) podemos colocar no gráfico, mas a situação se complica quando tentamos colocar f(x, y, z, t, ...) ou mesmo f(x, y, z). Porquê? Por que necessitam de mais um eixo perpendicular a os três já existentes, x (abcissas), y(ordenadas) e z(cota). Nossos sentidos e persepção não conseguem captar tal dimensão extra nem muito menos esboçá-la num papel em 2D.

O vídeo presente no link a seguir mostra essa relação. Clique aqui e veja: Entendendo a IV Dimensão

Entendendo a Trigonometria

Do grego "triângulo mais metron (medida)" a trigonometria é um ramo da matemática que estuda os triângulos e suas razões com os ângulos. Sua utilidade é vasta e sem dúvida é uma das mais requisitadas e estudadas áreas da matemática pelo seu grande número de serventias à outros campos.

Uma forma bastante fácil de se compreender a Trigonometria é a partir do triângulo Retângulo, ao qual possibilita trabalhar com alguns ângulos. Dele podemos suscitar hipóteses e conclusões que auxiliarão em muito a compreensão não só da sua relação com a geometria, mas também com as funções.

RELAÇÕES TRIGONOMÉTRICAS NO TRIÂNGULO RETÂNGULO

Quando se fala em trigonometria certamente também se está falando em ângulos. Uma forma prática de se conhecer as relações que existem entre eles é a partir de suas razões: seno, cosseno, tangente, cotangente, secante e cossecante.

* SENO

Diz-se que o seno de um ângulo é a razão entre o cateto oposto de uma triângulo retângulo por sua hipotenusa.

Seja o triângulo retângulo ABC, de lados a, b, c com hipotenusa a abaixo:

Figura 1: Triângulo Retângulo ABC e sua relação com o seno

* COSSENO
O cosseno de um ângulo é a razão entre seu cateto adjacente por sua hipotenusa. Este processo é análogo ao anterior. Seja o triângulo retângulo ABC, de lados a, b, c com hipotenusa a abaixo:

 Figura 2: Triângulo Retângulo ABC e sua relação com o cosseno

*TANGENTE
A tangente é a relação entre o seno e o cosseno de um determinado ângulo, ou ainda pode ser definida como a razão entre o cateto oposto de um ângulo pelo seu cateto adjacente. Análogo à figura anterior, fazemos:

O restante das relações, como cotagente, secante e cossecante serão oruindas das já vistas figuras 1 e 2.

* COTANGENTE

A cotangente mostra-se ser a razão entre o cosseno de um dado ângulo pelos seu seno, sendo, portanto, o inverso da tangente. Pode ser escrita assim:

* SECANTE

A secante é o inversa do cosseno, isto é,

* COSSECANTE

A cossecante é o inverso do seno, assim:

ÂNGULOS NOTÁVEIS

Existem alguns ângulos que são notáveis, isto é, se destacam dentro da gama de 360 ângulos que há. São eles, 30º, 45º e 60°, com seus respectivos múltiplos, ou côngruos com pequenas variações nos sinais, a depender de que quadrante se encaixam. Não está entendendo que história é essa de quadrante? Não se preocupe, aqui mostraremos do que se trata, mas antes vamos às relações que demonstram como surgiu os seno e cosseno desses ângulos. Vê-se que claramente não é preciso se calcular os valores da tangente, cotagente, secante e cossecante, umas vez que essas razões dependem apenas do seno e cosseno.

ÂNGULO DE 30°

Seja um triângulo eqüilátero de lados a, b e c, iguais, conforme figura abaixo. Por definição sabe-se que 
a = b = c. Dividindo esse triângulo ao meio numa altura h, um dos ângulos resultantes será 30º e os outros 60 º e 90º.

  Figura3: Triângulo equilátero

Seno

Como o sen30º = b/2/a,  e b = a, fica:

 

Cosseno

Como cos30º = h/a, é necessário encontrar o valor de h:

Por Pitágoras temos:

Donde,

Tangente
A tangente pode ser obtida como o quociente entre  sen30º/cos30º, ou na razão entre o cateto oposto pelo cateto adjacente, isto é, tg30° = a/2/h, donde,

Cotangente
A cotangete pode ser obtida através da razão inversa da tangente, isto é, cot30º = 1/tg30º, assim:

Secante
A secante consiste na razão inversa do cosseno, isto é, cosc30° = 1/cos30°. Fica:

Cossecante
O cossecante é a razão inversa do seno, isto é, cosc30° = 1/sen30°, assim:

Por processo análogo, encontramos os seno, cosseno, tangente, cotangente, secante e cossecante de 45°e 60° ou quaisquer outros graus, notáveis ou não. Deve-se colocar uma observação no ângulo de 45° que deverá ser demonstrado por outro tipo de triângulo distinto do da figura 3. Neste caso seria mais expressivo usar um triângulo retângulo isósceles, já que possui dois lados iguais e dois ângulos de 45°.



ANGULO DE 45°
Seja um triângulo isósceles com b = c ,abaixo, :

Sabemos que:

Seno 
O sen45° = c/a <=> b/a, a o que obtemos:

O seno de 45° é justamente igual a o seu cosseno já que os catetos oposto e adjacente são iguais, isto é:

Tangente
A tangente pode ser obtida como a razão entre o  cateto posto e o cateto adjacente, isto é, tg45° = b/b => 1 ou pelo quociente entre o sen45° e o cos45°, assim:

Cotangente
 Cotg45° =  1/tg45°
Cotg45° = 1




Secante
Sec45° = 1/cos45°, ou seja:

Cossecante
Cosc45° = 1/sen45°,donde resultará no mesmo valor anterior da secante, isto é:

As demais demonstrações angulares ficam a cargo do leitor que poderá fazê-lo como exercício do exposto aqui.

Todas as razões apresentadas anterioremente também tem comportamentos distintos quando inseridos nos gráficos constituindo-se, portanto, funções trigonométricas. Cada função tem um campo definido de seu domínio e a depender do sentido de rotação podem ser positivos ou negativos.

FUNÇÕES TRIGONOMÉTRICAS

Ainda em construção...

O Desafio Matemático do Ensino Superior

Sem dúvidas é um terrível sacrilégio para quem entra pela primeira vez no Ensino Superior quando se depara com o ensino da matemática. De cara já vê assuntos complicadíssimos para uma formação mediana, como limites, derivadas, integrais e álgebra. Além das inúmeras funções que tem de dominar absolutamente, ainda existe o medo das provas que são extremamente exigentes com altos níveis de acertos.

Mas quem acaba de entrar numa Faculdade onde a matemática faz parte da grade curricular como base, vai um lembrete: É preciso, antes de tudo, amar a disciplina para ser bem sucedido nela. Os cursos de Administração,Contabilidade, Geografia, Oceanografia são alguns dos que envolvem a matemática, mas há ainda aqueles que labutam diretamente com ela em níveis altíssimos, como as Engenharias (de pesca, da computação, civil, elétrica, mecânica, ambiental e outras) bem como Matemática, Física e Astronomia são algumas terrivelmente recheadas de cálculos.

Nessas últimas é que vem a peleja. Lidam com matemática pura quase que o tempo todo, e logo nos primeiros períodos os alunos são bombardeados com equações de todos os lados e iniciam de uma forma dura e direta. Cálculo I, nome de umas das disciplinas, é feroz e devora praticamente quase que metade de uma turma. Há casos de classes que perderam em um dos Cálculos I, II, III ou IV, quase que inteiras, passando apenas alguns dois ou três! O estudo de limites até que não é complicado, mas quando inserido às derivadas e integrais, surge a necessidade imperiosa de um conhecimento matemático refinadíssimo, pois explora funções e uma trigonometria  monstruosa, além de um mais que ecxelente nível de geometria plana, espacial e analítica, sem mencionar a álgebra envolvida com seus vetores, planos uni, bi, tri e multi dimensionais. É um terror, mas extremamente necessários, o que exige uma dedicação muito grande dos estudantes, com horas e horas de estudos, se não: Final, na melhor das hipóteses.

A maioria das Universidades não admitem que qualquer um faça a final de alguma disciplina sem antes alcançar uma certa nota. Por exemplo, em muitas Instituições são cobradas duas avaliações no valor de 10 pontos. Se o estudante tirar, em ambas as provas, menos que seis pontos, não vai para final, perde direto!

Imagine isso com as ciências exatas e que na sua imensa maioria são pré-requisitos! E há Universidades que cobram pontuações mais altas, como sete, para conseguir a chave da prova final!

Pré-requisitos são aquelas matérias que não podem ser cursadas sem que antes o candidato a ela tenha sido aprovado por outra anterior. Exemplo: Um certo estudante perdeu em Análise I e ela é pré-requisito para Análise II. Este não fará Análise II enquanto não pagar Análise I. E a situação piora quando uma só disciplina é pré-requisito para mais de uma! Geralmente Cálculo I é pré-requisito para Análise. Não só Cálculo I, mas o II, III ou IV. Então se não pagar Cálculo I, não paga Cálculo II, nem o III, IV ou a  algumas das Análises. Agora deu para entender porque todo universitário só vive estudando e sofrendo? Também deu para entender porque quando eles fazem aquelas festinhas, normalmente nunca saem no diminutivo, mas são verdadeiros carnavais?

O desafio hoje no Ensino Superior nas Exatas consiste em reduzir as baixas notas sem reduzir a qualidade do ensino formando pessoas capazes e gabaritadas ao exercício ao qual foram preparadas. E mais, não deixar de investir em mais recursos pedagógicos e tecnológicos para sempre acompanhar a modernidade e suas mudanças. Infelizmente o primeiro e mais fundamental passo é o mais difícil. A evasão nesses cursos é muito grande e o número de formandos menos ainda. Isso implica numa baixa injeção de pessoas habilitadas em tecnologia e que poderia estar produzindo mais tecnologia e progresso para a nação. Parece ser um papo meio repetitivo, mas é a pura verdade. Não basta apenas formar, é necessário ter uma boa qualidade, investir e acompanhar as mudanças.

O Fantástico Euler

Leonard Euler foi um notável matemático suíço que viveu no século XVIII. Autor de mais de 886 trabalhos matemáticos, foi ele quem deu  origem às atuais formas de escrever as funções em f(x), o número Pi, redescobriu o Phi, as formas complexas, as raízes de graus n>3, implementou, aprimorou e descobriu os Número de Euler, Números Eulerianos, Fórmula de Euler, é considerado o pai da análise matemática, sendo importante com notáveis contribuições nos campos da física, astronomia, música, matemática e engenharia.

Figura 1: Leonard Euler

Um gênio completo que a os dezessete anos alcançou seu mestrado e tinha aulas nada mais nada menos que com Johannes Bernoulli. A os dezenove anos recebeu uma menção honrosa por uma solução de um problema proposto pela Academia de Paris e mais tarde ganhou seu primeiro prêmio nesta mesma academia 12 vezes. Tinha uma memória fora série: Recitava a famosa Eneida de cor, e numa ocasião entre uma pequena disputa de alguns de seus pupilos, calculou de cabeça até a  quinquagésima casa decimal do número de euler. Ver abaixo a posição do número que ele calculou de cabeça:

2.71828182845904523536028747135266249775724709369995

Mesmo depois de cego continuou produzindo e metade de suas contribuições científicas deu-se nesse período.

OBRAS

A obra euleriana é tão vasta que mesmo 50 anos após a sua morte, a Academia de São Petersburgo continuava a publicar alguns de seus artigos que ainda estavam engavetados. Com uma média assombrosa de cerca de 800 páginas por ano durante toda a sua vida, mesmo depois de cego, conseguiu contribuições notáveis. Veja alguma delas:

=> Notação Matemática

A matemática possui uma linguagem simples, mas como qualquer forma "lingüística" necessita de que seja conhecida para maior entendimento coletivo. Alguns dos mais usados termos matemáticos fora introduzido por esse gênio, como:

* O símbolo "e" da base dos logaritmos neperianos.

* O símbolo para   π (pi) ,designa a razão entre a circunferência e o diâmetro do círculo

* O símbolo "i", para denotar a unidade imaginária do Corpo dos Números Complexos

* Letras minúsculas como a, b e c, para representar os lados de um triângulo e letras maiúsculas como A, B e C para representar os seus ângulos opostos.

Além dessas existem outras infinidades de símbolos criados por Euler para facilitar a vida dos matemáticos. Mas não parou só nisso:

=> Equações

Introduziu equações Notáveis que são usadas nos campos da física, astronomia, engenharia, música, meteorologia e, claro, matemática. Certamente uma das mais notáveis é a expressão abaixo considerada por muitos matemáticos de todo o mundo como a equação mais linda dentre toda a matemática:

Considera-se tão linda tal equação por poder resumir, numa só expressão, os principais fundamentos matemáticos, como o "e", base dos logaritmos neperianos, o "i", representando os imaginários do Corpo dos Complexos, o pi, representando a geometria, o 1 e o zero representando a aritmética com o sinal de igualdade, unindo tais áreas. É vital saber que o número de euler é irracional, isto é, não pode ser escrito na forma p/q, quando q diferente de zero. Em outras palavras, um número irracional não pode ser escrito em forma de fração, mas isto não quer dizer que não possa ser calculado.


Aqui estão algumas de suas criações: Introductio in analysin infinitorum; Institutiones calculi differentialis; Institutiones calculi integrali; Theoria motus corporum solidorum seu rigidorum; Mechanica; Letters to a German princess, além das Teorias da adição de séries; teorema das pontes de Königsberg.


Contribuições na Trigonometria, geometria, análise, equações diferenciais, e teoria dos números bem como física, química e astronomia forma esse gênio numa verdadeira lenda humana! Euler foi prodigioso, gênio, uma mente aguçada e anos luz à frente de seu tempo. Certamente uma das figuras que merecem respeito na Comunidade Científica, na matemática e na mente das pessoas.

A Mãe de Todas as Equações - A Grande Teoria do Século

Durante muito tempo físicos de todo o mundo sonharam com uma teoria que unificasse todas as outras teorias existente, uma espécie de equação matemática mãe, que resumisse em si todas as outras fórmulas existentes. Figuras famosas como Albert Einstein também acreditaram nessa teoria  e empenhou arduamente muitos anos de sua vida na sua descoberta que infelizmente não culminou com sua resolução.

Para quem não está entendendo o que se está dizendo, é o seguinte: Físicos sonham com uma Teoria que possa englobar tudo, uma só equação, ou conjunto de regras que possam explicar todos os fenômenos que ocorre no Universo, desde os cosmológicos a os quânticos.

Quando Isaac Newton desenvolveu suas Três Leis, ele explicou muitos acontecimentos, como o porquê maçã cai, a Lua não cai sobre a Terra, as forças que interagem com a massa e a aceleração por meio da fórmula   F = m.a e afirmou que toda ação produz uma reação de mesma força e sentido contrário, observações essas confirmadas e evidenciadas por experimentos. De certa forma, Eisntein, com as Teoria da Relatividade Geral e Especial também quebrou elos fantásticos da gravitação Newtoniana e a complementou de modo assustador, mas deixou de fora toda a mecânica quântica de outro grande gênio, Heisenberg. Observações efetuadas por Galileu, e os notáveis avanços da  matemática (com o rigor proporcionado e criado por Leonard Euler)  fecundaram  um terreno rico de imaginações e descobertas importantes.

Imagine o leitor uma fórmula capaz de descrever tudo o que ocorre na Terra -o atrito, o som, a luz, os foguetes, a Lua - fenômenos que assumem juntos pelo menos quatro forças fundamentais: gravitação, força nuclear forte, força nuclear fraca e eletromagnetismo, todos juntos. Parece fácil, mas tal desafio consiste num dos maiores mistérios do conhecimento científico humano até o momento. Há quem diga que tal Teoria é impossível, um sonho em vão dos físicos e matematicamente improvável.

Figura 1: Alguns gênios e sua contribuições: Isaac Newton, Albert Einstein, Leonard Euler e Galileu Galilei

Ainda, segundo modernas teorias, o Universo assumiu uma cara multi facetada, já que a Teoria das Super-Cordas e subjacentes estão na moda com possibilidade de explicar tudo numa só cartada.

Querendo ou não o sonho dos físicos tem de culminar com uma fórmula matemática elegante, compreensível e constatada. Ela, a matemática, exige rigores extremos e não admite "achismos", sendo, portanto, uma poderosa ferramenta a favor de quem deseja a "verdade" do Universo. Pode parecer trivial e sem sentido, mas recentemente um grupo de 18 matemáticos e cientistas de informática resolveram, ao longo de 4 anos com o recurso de um monstruoso computador, uma estrutura matemática secular.

O que impressionou foi que a tal estrutura, a E8 (pertencente ao grupo de Lie), mostrou-se ser 60 vezes maior que o código genético humano, e absurdamente cobriria, se colocado seus dados na menor fonte de letra, toda a área de Manhattan, nos Estados Unidos. O que isso tem a ver com a Teoria do Tudo? Estudiosos afirmam que a descoberta da solução desse intrigado problema matemático pode sugerir uma luz de maior intensidade das idéias modernas, isto é, sua descoberta possui vastos campos de atuação e cabe a os cientistas descobrirem as razões, sem falar que a tal da E8 abriga cerca de 248 dimensões. Para se ter uma idéia no mundo "real" só pode ser visto três dimensões, e uma quarta dimensão, que apenas as equações sugerem haver. É impossível, até o momento, de se visualizar, sendo extremamente complicado só pensar, imagine de se ver!

Figura 2: E8, estrutura matemática do Grupo de Lie com 248 dimensões
  

Muitas das atuais teorias se baseiam em  várias dimensões, além das três + 1 conhecidas, o que pode acarretar numa soma de dados, provenientes da E8, que possa ajudar nessas descobertas, um avanço incalculável!

Uma Análise Matemática do Arco da Orla de Curaçá

Na nossa cidade (Curaçá-Ba) existe uma figura geométrica que muito intriga. Para alguns não passa de uma estrutura em forma de arco, mal feita e que enfeita a orla. Para outros representa uma forma peculiar de arquitetura. valorizando o por do sol trazendo uma estética arrojada à visão de quem a observa de frente.

Figura 1: Arco da Orla de Curaçá, visão de frente ao por do sol

Fato é que tal estrutura cativou a curiosidade matemática desse que vos escreve, e a pedido de uma amigo, resolvi fazer uma pequena pesquisa do arco.

Os resultados não se mostraram ricos, tamanho também foi o desânimo quando vi que se tratava de um objeto geométrico irregular e grosseiro. Mas quão foi admirável quando, na verdade, verificou-se de que não se tratava de uma parábola. Vamos a os dados:

* O arco não é uma parábola

*  O arco cria uma ilusão de um "arco capaz"

* O sol fica bem no meio do arco nos solstícios apresentando belas imagens

* Tem traços fortíssimos da Razão Divina

Bom, vamos  falar do nosso primeiro item.

=>PARÁBOLA

Aprendemos no ensino fundamental que uma equação de segundo grau tipo ax² +bx + c forma no gráfico uma parábola, que pode ter uma máximo, se está voltada para baixo, ou pode ter um mínimo, se está voltada para cima. É verificável que o referido arco se encontra voltado para baixo, logo tem um máximo, que é o seu topo, só que não se configura uma parábola. Por que então não pode ser considerada tal?

Uma parábola tem suas "pernas" sempre abertas se dirigindo ao infinito não paralelas. O que se observa na estrutura é que as suas "pernas" deixam a inclinação natural em direção ao infinito e ficam em linha reta com o solo. Mais estudos poderiam supor que ao invés de ser parábola, ela poderia ser uma elipse. Isso exigiria mais um pouco de estudos.

Figura 1.2:Diferenças entre Arco e parábola, respectivamente.

Não se sabe qual a intenção do arquiteto que a criou, mas certamente quem pensa que ela é semelhante àqueles gráficos quadráticos que se vê na 8ª (oitava) série, apenas colide com a semelhança, que se perde no rigor matemático. O arco não é uma parábola.

 Figura 1.3:Pernas da parábola indo ao infinito e não paralelas.

=>ARCO CAPAZ

O arco capaz é uma arco que tem a propriedade de ser observado, a qualquer ponto de um  mesmo determinado ângulo escolhido. O da Orla não é um arco capaz, pois não é capaz de proporcionar, a diferentes observadores em nenhum ângulo, a mesma paisagem propiciada. Em outras palavras, se fosse um arco capaz, ele proporcionaria a mesma visão a diferentes observadores em diferentes ângulos.

=> IMAGEM DO POR DO SOL

Em certas épocas do ano é possível deslumbrar, a certo ângulo, um por de sol diretamente no centro desse arco. A figura 1 mostra esse fenômeno quase no seu ápice, sendo infeliz na escolha do ângulo para flagrá-lo no meio. Mesmo assim a vista proporcionada é belíssima, levantando suspeitas de ter sido construído em base da razão divina.

=> RAZÃO ÁUREA

Também chamada de Razão Divina. Número de Outro, Razão Dourada, o número oriundo da divisão de certos tamanhos, propicia uma dos mais incríveis e misteriosos dentro da matemática, o número phi.

Estudado pelos gregos foi fundamental nas construção de vários templos dos deuses na antiga Grécia, como o Parthenon, arquitetado todo dentro dessa razão. Os pitagóricos também gostam dessa razão e estudavam a fio as propriedades desse estranho número, 1, 608..., que é irracional. Ele está presente na natureza através as flores, árvores, animais, furacões, tufões, e também no homem.

O arco parece possuir as mesmas características áureas, nome dado por conta de os gregos a europeus na Idade Média acharem-no divino, obra de Deus.O ângulo de formação dos pés da estrutura se aproxima razoavelmente dessa razão, e sua visão quando o sol descamba também alude ao tal divino número. No entanto mais observações e medições são necessárias a serem efetuadas a fim de que possa se constatar se foram colocados de modo proposital ou apenas uma feliz coincidência.

Ora, como coincidência, podem afirmar alguns. O curioso é que muitas pessoas desenham e fazem obras de arte em cima dessa razão e não sabem. Quando determinada figura, imagem, construção sai-se muito bonita, de modo agradável a os olhos humanos, quase sempre, quando se faz uma análise matemática, resulta no número divino! E mais, é perceptível que o arco fica numa distância que entre o começo e fim da orla cimentada, que se aproxima terrivelmente da razão áurea, isto é, a distância entre o arco e o começo da Orla contando a partir do prédio da Secretaria de Educação, e a distância entre ela o fim da orla, próximo ao bar de Cachoeira, se divididas, maior parte pela menor parte, resultar-se-ia na tão famosa razão citada!

Será o Arco da Orla, uma estrutura divina? Depende dos olhos de quem vê.

Mais detalhes da Equação que descreve o Arco, clique aqui e faça o download em Word do arquivo preliminar que será mais profundamente analisado pelos alunos da 8ª série B da Escola Estadual Dr. Manoel Novaes de Curaçá - BA. Após ir à página direcionada escolha o formato doc e a opção download now, escolha o local de armazenamento ou peça para abrir e pronto, está em posse do artigo.

PRÓXIMO ARTIGO DISCUTIREMOS A MATEMÁTICA EXISTENTE NO PRÉDIO DA BIBLIOTECA MUNICIPAL E O ESTRANHO CILINDRO DE PORTA. Quantos litros de água será que cabe lá?

O Segredo Oculto dos Números Complexos

 

Você sabe qual é a raíz quadrada de -4? Essa aqui, mostrada abaixo?

Ora, quando perguntados qual a raíz quadrada de 4, todos responderiam que seria 2, porque 2 X 2 = 4. Mas o que acontece quando temos uma negativa, como a descrita acima? Veja:

Estranho, quando -2 é multiplicado por ele mesmo duas vezes, fazendo o jogo de sinais, ele fica positivo, diferenciando de -4, que seria o número que deveria dar.

É comum na 9º (nona) série do ensino fundamental (antiga 8º série) alunos se depararem com raízes de números negativos quando estão vendo equações de segundo grau. Geralmente quando chegam nessa parte, alguns professores evitam de se aprofundar no tema e simplesmente dizem a os alunos que não existe raíz de número negativo, e mais comum ainda dizerem apenas raíz, colocando até as raízes cúbicas em demais ímpares, o que é um erro crasso! 

Então, como calcular uma raíz negativa dessas?  Bom, primeiramente, antes de responder, é preciso conhecer alguns fatos importantes, pois este é um segredo oculto do Conjuntos dos Números Complexos, assunto abordado apenas no terceiro ano do ensino médio.

BEM VINDO A OS NÚMEROS COMPLEXOS

Ignorado por muitos séculos como sendo parte banal de alguns cálculos que exigiam raízes negativas, os matemáticos nem se quer perdiam tempo em analisar os famosos complexos, sutilmente apelidados de números fantasmas justamente por não fazerem "sentido". Somente mais tarde, com a pequena menção, mas sem explicações de um artigo publicado pelo matemático Cardano, é que apareceu os temidos e evitados  complexos. Contudo apenas com Raphael Bombelli, outro notável matemático é que não só teve a mesma coragem demonstrada por Cardano, mas também os explicitou introdutoriamente.

Para se ter uma idéia do que estamos falando, há relatos dos cujos números desde a Arithmetica de Diophanto a aproximadamente no ano de 275 D.C, no começo do primeiro milênio que mesmo assim também evitou de falar no assunto, ficando os Números Complexos à mercê da ignorância de tantos séculos e homens que negaram-se a ouvir os gritos de umas das mais importantes classes de números da humanidade. Mais tarde, num estudo das equações de terceiro grau é que praticamente a humanidade viu-se obrigada a admitir os complexos, finalmente reconhecidos. Agora podemos conhecer também esses temíveis números e saber por qual motivo os escondiam bastante.

O QUE É UM NÚMERO COMPLEXO?

Um número complexo é basicamente um conjunto, um corpo maior dos números, maior até mesmo que os conjunto dos números Reais, que praticamente abriga quase a totalidade dos mesmos.Segundo Gelson Iezzy, "chama-se conjunto dos números complexos, e representa-se por C, o conjunto dos pares ordenados de números reais para os quais estão definidas a igualdade, a adição e a multiplicação" (IEZZY, Gelson, pág. 2, 1998).

"Encara-se assim R como um subconjunto de C", afirma Lipschutz o que é confirmado pelas operações envolvidas nos processos de cálculos algébricos efetuados com esses números. Basicamente escrevemos um complexo algebricamente como Z = a + bi, ou por par ordenado como Z = (a, b) onde a é a parte real e b, a parte imaginária e Z o número complexo.

É perceptível que que a afirmativa de Lipschutz é verdadeira quando o valor de b é zero, pois fica somente a parte real, como o são a maior parte dos números com vemos.

Seja a = 2 e b = 0. Como escrevemos esse número, que é real, em complexo?

Ora,

Z = a + bi, então:

Z = 2 + 0.i

Z = 2

Quando isso ocorre dizemos que o dado número é um Real puro. Mas o que acontece quando b = 0?

Seja a = 0 e b =2

O processo é análago a o anterior

Z = a + bi

Z =  0 + 2i

Z = 2i

Agora dizemos que Z é um imaginário puro.

Quando há os dois valores, com a diferente de b e ambos diferentes de 0, o complexo está completo, assim:

Z = 2 + 2i, 

Que pode até ser a solução daquele probleminha de equação quadrática de delta negativo!

RESOLVENDO RAÍZ DE NÚMERO NEGATIVO 

A o longo dos séculos era impossível resolver esse tipo de equação:

x² + 2x + 2 = 0, porque o valor de delta é menor que 0.

Adequando os valores dos coeficientes e resolvendo a equação, temos:

 

Entretanto, com o advento dos complexos, permitiu-se, assim, que se prosseguisse a operação. Repare bem que - 4 é o mesmo que escrever - 4 = (- 1).4 . Como 4 tem raíz e é 2, extrai-se esse número e - 1 que "não tem" fica dentro da raíz. Convencionou-se chamar essa raíz de - 1 de i, e se colocarmos ele ao quadrado daria justamente um númewro real, donde:

Gerou-se duas raízes Complexas. O curioso é que não foi por causa das equações quadráticas que se empenharam em descobrir os complexos não, mas sim com as equações de terceiro grau!

OPERAÇÕES COM NÚMEROS COMPLEXOS

Como qualquer número podemos somar, subtrair, multiplicar e até dividir números Complexos. 



* Adição

Propriedade:
Seja Z1 = (a, b) e Z2 = (c, d). Z1 + Z2, fica:

(a, b) + (c, d) = (a + c, b + d), formando um par.


Seja Z1 = 3 + 4i e Z2 = 7 + i. Determine Z1+ Z2.

Há duas formas de se calcular e uma delas é pelo seu par ordenado. Como vemos, um par ordenado se dá através da separação em parte real e imaginária. Z1 = (3, 4) e Z2 = (7, 1). Somando, fica:

Z1 + Z2 = (3 ,4) + (7, 1) = (3 + 7, 4 + 1) => (10, 5) completando o par ordenado. Também poderíamos fazer direto:

Z1 + Z2 = 3 + 7 + 4i + i => 10 + 5i

* Subtração 

Propriedade:

Seja Z1 = (a, b) e Z2 => (c, d). Z1 - Z2, fica:

(a, b) - (c, d) = (a - c, b - d), formando um par.

Seja Z1 = 3 + 4i e Z2 => 7 + i. Determine Z1- Z2.

Fica:

Z1- Z2 = (3 - 7, 4 - 1) => (- 4, 3) ou

Z1- Z2 = 3 - 7 + 4i - i => - 4 + 3i

* Multiplicação
Propriedade:

Seja Z1 = (a, b) e Z2 => (c, d). Z1. Z2, fica:

(a, b).(c, d) = (ac - bd, ad + bc), formando um par.

Seja Z1 = 3 + 4i e Z2 => 7 + i. Determine Z1. Z2.

Fica:

Z1.Z2 = (3.7- 4i.i, 3i + 4i.7) => (21 -(- 4i²), 3i + 28i), como i² = - 1, obtemos:

 Z1.Z2 = (21 + 4, 31i) => (21-4, 31i), que resulta em:

Z1. Z2 = (17,  31i)

Essa forma que acabamos de explicitar é a forma ordenada. Também é possível encontrar o mesmo valor multiplicando pela forma algébrica, assim: 

Z1.Z2 = (3 + 4i).(7 + i)  

Z1.Z2 = 21 + 3i + 28i  + 4i²

Z1.Z2 =  21 - 4 + 31i

Z1.Z2 =  17 + 31i

* Divisão

Propriedades:

Seja Z = a + bi, há um conjugado de mesmo módulo mas de sinal de bi diferente. A esse chamamos de conjugado e se escreve assim:   −Z = a - bi. O conjugado serve principalmente para se efetuar e simplificar alguns números complexos.

Seja Z = 2 + i/3 + i. Determine os valores de a e b do complexo dado.

 Ora é visível que não dá para saber quem é a ou b porque eles estão misturados no numerador e denominador. Antes, porém, é preciso que se separe ele da maneira usual Z = a + bi, mas para fazer isso é preciso dividir, e para dividir é necessário multiplicá-lo pelo conjugado do número de baixo, assim:

Z = (2 + 3i)(3 - i)/(3 + i)(3-i). 

Efetuando a multiplicação, obtemos:

Z = 9 + 7i/10, portanto:

a = 9/7 e

b = 7i/10

Apelidado de Números Fantasmas durante muito tempo, os então hoje conhecidos Conjunto dos Números Complexos conheceram bem o peso do preconceito intelectual.



Forma Polar
 
Muitas vezes não podemos expressar determinados complexos por sua forma algébrica Z = a + bi. Ocorre em inúmeros casos onde Z assume valores com altos expoentes, ou porque é melhor para se aplicar em certas operações matemáticas, sendo mais fáceis de se lidar e manusear.


Podemos determinar como forma polar se ela pode ser escrita na forma Z = p(cosx + isenx), onde p (lê-se rô). p = √a² + b²

Obtemos-no-la através da seguinte demonstração:

Algumas Questões do Enem 2008

Bem, aqui se dará início a uma série de resoluções de algumas das mais interessantes questões de matemática do Exame Nacional do Ensino Médio de 2008, o Enem.

Nesse Enem há diversas questões que direta ou indiretamente, envolvem matemática, mas aqui será postado apenas as mais interessantes ou trabalhosas de resolução. Quem desejar ver outros tipos, seja do ano passado, ou de anos anteriores, basta deixar abaixo um comentário, especificar o ano e cor da prova e o quesito do Enem que deseja. Pode também mandar questões de vestibulares.

Bom, vamos lá!

Começando pela questão 21 da prova amarela. A escolha da prova de cor amarela se dá devido ser esta a cor oficial de correção.

Questão21

O tangram é um jogo oriental antigo, uma espécie de quebra-cabeça, constituído de sete peças: 5 triângulos retângulos e isósceles, 1 paralelogramo e 1 quadrado. Essas peças são obtidas recortando-se um quadrado de acordo com o esquema da figura 1. Utilizando-se todas as sete peças, é possível representar uma grande diversidade de formas, como as exemplificadas nas figuras 2 e 3.

Se o lado AB do hexágono mostrado na figura 2 mede 2 cm, então a área da figura 3, que representa uma “casinha”, é igual a:

A 4 cm2. B 8 cm2. C 12 cm2. D 14 cm2. E 16 cm2.


RESOLUÇÃO:

Repare que a medida do lado AB da figura 2 mede exatamente 2cm e que todas as figuras, (1, 2 e 3) possuem as sete figuras geométricas que formam o tangran. Claro que a figura 1 é a mais fácil de se calcular uma área, pois esta é um quadrado perfeito, mas antes, é preciso saber sua medida de lado. Repare na figura a seguir que o quadrado e o triângulo que unidos resultam em 2cm estão marcados de vermelho, que é justamente metade do quadrado (figura 1).

Chamando de "l" as medidas do quadrado, que não sabemos ainda, e de 4 a diagonal total (existem duas partes iguais a 2), pelo Teorema de Pitágoras fica:

a² = b² + c²

4² + l² + l²
16 = 2l²
2l² = 16
l² = 16/2

l² = 8

Ora, como a medida da área de um quadrado é o quadrado de seu lado, A = l²
temos que:

A = 8
Respota B

QUESTÃO 16

O sistema de fusos horários foi proposto na Conferência Internacional do Meridiano, realizada em
Washington, em 1884. Cada fuso corresponde a uma faixa de 15º entre dois meridianos. O eridiano de Greenwich foi escolhido para ser a linha mediana do fuso zero.

Passando-se um meridiano pela linha mediana de cada fuso, enumeram-se 12 fusos para leste e 12 fusos para oeste do fuso zero, obtendo-se, assim, os 24 fusos e o sistema de zonas de horas. Para cada fuso a leste do fuso zero, soma-se 1 hora, e, para cada fuso a oeste do fuso zero, subtrai-se 1 hora. A partir da Lei n.° 11.662/2008, o Brasil, que fica a oeste de Greenwich e tinha quatro fusos, passa a ter somente 3 fusos horários.
Em relação ao fuso zero, o Brasil abrange os fusos 2, 3 e 4. Por exemplo, Fernando de Noronha está no fuso 2, o estado do Amapá está no fuso 3 e o Acre, no fuso 4.
A cidade de Pequim, que sediou os XXIX Jogos Olímpicos de Verão, fica a leste de Greenwich, no fuso 8.

Considerando-se que a cerimônia de abertura dos jogos tenha ocorrido às 20 h 8 min, no horário de Pequim, do dia 8 de agosto de 2008, a que horas os brasileiros que moram no estado do Amapá devem ter ligado seus televisores para assistir ao início da cerimônia de abertura?


A) 9 h 8 min, do dia 8 de agosto.
B) 12 h 8 min, do dia 8 de agosto.
C) 15 h 8 min, do dia 8 de agosto.
D) 1 h 8 min, do dia 9 de agosto.
E) 4 h 8 min, do dia 9 de agosto.

RESOLUÇÃO

Essa é a típica questão que exige bastante atenção e uma boa leitura e também ,por isso ,carrega uma pequena casca de banana nela.
Considerando que Greenwich é o marco zero, e que todo meridiano contado à direita soma-se 1 hora, e que todo meridiano contado à esquerda subtrai-se 1 hora, e que Pequim está a 8 fusos á direita (leste em relação a Greenwich), e que o Amapá está a 3 fusos à esquerda de Greenwich (à oeste), fazemos:

8 + 3 = 11, o que corresponde a 11 horas, que não é o suficiente para dar mais de um dia.
Como os jogos começariam às 20h e 8 min do dia 8 de agosto de 2008, e que seu local de realização está à direita do Amapá, contanto de Pequim até o Brasil, isto é, para oeste, subtrair-se-ia os valores, assim:

20h e 8 min - 11h = 9h e 8 min do dia 8 de agosto de 2008.

ALTERNATIVA A

QUESTÃO 33

A figura abaixo representa o boleto de cobrança da mensalidade de uma escola, referente ao mês de junho de 2008.

Se M(x) é o valor, em reais, da mensalidade a ser paga, em que x é o número de dias em atraso, então

A M(x) = 500 + 0,4x.
B M(x) = 500 + 10x.
C M(x) = 510 + 0,4x.
D M(x) = 510 + 40x.
E M(x) = 500 + 10,4x.

RESOLUÇÃO

Essa é a típica questão de função do primeiro grau tipo y = ax + b

Sabemos, pela figura do boleto bancário, que há um valor constante, que não se altera se houver um atraso, que é de R$ 500,00 + multa de R$ 10,00, o que nos dá um total de R$ 510,00 constante, que tem de pagar de qualquer forma. Como ainda há 40 centavos de multa por atraso por dia, fica:

y = 510 + 0,4x

ALTERNATIVA C