Calculando o Infinito

A Integral

Ao longo dos séculos o homem sentiu necessidades imperiosas da obtenção do valor exato, ou pelo menos aproximado, de algumas áreas e/ou volumes de certas figuras geométricas com  contornos irregulares. Ele já sabia calcular áreas e volumes de figuras regulares, como cones, pirâmides, cubos, prismas, esferas entre outros, não obstante outros tipos de figuras continuavam sem esclarecimento.

Com a chegada de Isaac Newton e Leibniz essa história começou a ser contada de um novo capítulo, com a introdução do Cálculo Diferencial e Integral.

Aqui nos concentraremos em demosntrar a definição técnica da Integral não contendo, porém, os principais meios de resolução destas, que será mais bem tratado em outro artigo.

Basicamente esse cálculo consiste no estudo de uma dada função f(x) definida no intervalo [a, b], conforme figura a seguir:

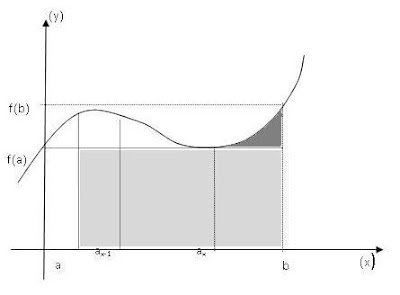
A idéia é de obter a área da região hachurada da figura ao lado. 

Como pode ser observado uma parte da área, a de cor mais fraca, forma um retângulo que pode ser calculado através de (b - a)(f(a) - 0), contudo ainda resta a parte da área compreendida entre f(b) e f(a), com mesmo domínio fechado de [ax, b]. A parte de cor mais forte tem contornos irregulares que tornam seu cálculo muito complicado. Como então obter seu valor exato?

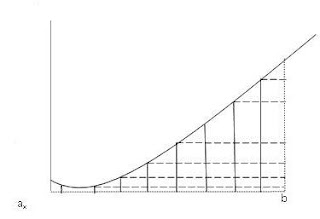
Dividindo-se o gráfico em pequenas partes é possível obter a área dessas pequenas partes divididas, assim:

É o somatório dos pequenos retângulos em escalas cada vez menores que definirá o valor da área final. É perceptível que quanto mais se quebre o gráfico em pequenos gráficos e o amplie, cada vez mais retângulos e áreas semehantas à de cor mais forte do primeiro gráfico vão se gerando, e assim até o infinito. Há um ramo dentro da matemática capaz de determinar valores que tendem ao infinito e é através do estudo de Limites.

Assim sendo podemos dizer que uma Integral é definida por:

Esta última notação da equação acima é como se escreve, matematicamente, uma integral, que significa literalmente somar partes, seja para áreas, volumes ou quaisquer cálculos que requeiram somatórios.

Bom como já visto é preciso que a função seja definida no irtevalo fechado [a, b] e que seja contínua. Uma vez tendo esses atributos o próximo passo é verificar que tipo de função se está usando e é aí que está o problema: Existem diversas maneiras de se trabalhar com integrais e cada uma deleas requer um tipo de especial de resolução ou estratégia.

TIPOS DE INTEGRAIS

Existem as Integrais Definidas, que são como essas estudadas anteriormente em que é preciso os valores dos limites do domínio ou da imagem da função, e também as Integrais Indefinidas, que não precisam de um intervalo fechado. Ora, essa última serve mesmo apenas de conhecimento teórico uma vez que sem um intervalo não é possível se calcular com precisão nada. Em exercícios é comum o uso desses tipos de Integrais, mas para o uso devido na vida prática é preciso a existência do intervalo.

Há ainda as Integrais resolvidas por Substituição, as Parciais, Polares, por Partes, entre outras. Estamos falando aqui dos tipos de resoluções dessa poderosa arma da matemática que será tratado em breve aqui.



CURIOSIDADE
PRATO DO DIA: PLANETA ASSADO

Plantas carnívoras, animais canibais, guerra por alimento. Tudo isso parece ser imensamente terráqueo, mas quem pensa que é só na Terra que há matanças está enganado.

A imagem abaixo ilustra o apetite voraz de uma estrela que rouba, a cada tempo que se passa, mais e mais gás de um planeta em sua órbita pois o dito cujo se trata de um corpo gasoso que só não é classificado como estrela por não possuir massa suficiente para as mesmas, mas que possui temperautra semelhante a o de uma pequena estrela fria.

Créditos da Imagem: (BARBOSA, Cássio, Jornal G1- Globo)

Com futuro bem perto das entranhas dessa estrela, o nosso planeta acima figurado tem seus dias contados até sua digestão. O interessante é que fatos como esse não são raros no Universo. Há diversos tipos de exemplos de não só estrelas engolindo planetas, mas também de estrelas engolindo estrelas, galáxias engolindo galáxias e até nmesmo aglomerados de galáxias inteiras sendo comidas por outras galáxias. Canibalismo até no espaço!