Geometria Analítica: Reta e Plano

Apresentaremos agora uma breve noção do que é a Geometria Analítica aplicada ao Plano e a Reta do R³ aliado ao conceito de vetores e suas características mais usuais.


1. APRESENTAÇÃO DO PLANO OXYZ.

Pouco se fala, em nível médio, sobre coordenadas em três dimensões. Geralmente o que se aplica nesse nível se baseia no R², i.e, em duas dimensões simbolizados pelas retas x (abcissas) e y (ordenadas) colocadas perpendicularmente uma a outra cujas coordenadas são dispostas em diversos pontos nesse espaço, como por exemplo aos pontos P(2,3) e Q(3,2), pertencentes a esse espaço. Contudo, aqui, exploraremos essas mesmas propriedades a nível de três dimensões, ou seja, agora além de "x" e "y" teremos também "z" (cota), perpendiculares entre si, como na figura: 

Fig. 1: Plano Oxyz

Pela figura 1 vemos como estão distribuídos alguns pontos no plano. Temos o ponto P1 de coordenadas (x, 0, 0), por isso marcado apenas no eixo das abcissas. Também os pontos P2 e P3. O ponto Q0 já possui valores para x, y e z, que são representados por   x´, y´e z´, ambos pertencentes a Oxyz com x < x´, y< y´e z < z´ na parte positiva do plano. Lembre-se de que O é a origem. 

Quando dados os pontos, os valores de x´, y´e z´ terão valores numéricos reais. Por exemplo, o ponto Q poderia ter coordenadas Q (1, 2, 3).

2. VETORES

2.1 IDENTIFICAÇÃO DE VETORES

Um vetor pode ser representado por um segmento de reta orientado. Em matemática pode ser um ponto, à partir da origem, ou o segmento de reta definido entre dois pontos com tamanho, direção e sentido. Ver figura 1.1:

Fig. 2.1: Vetor u = B - A definido pelos pontos A e B

Quando um segmento de reta é delimitado por dois pontos quaisquer, como na Fig. 2.1, identificamos o vetor como a diferença entre os pontos, ou seja, o vetor u = B - A, i.e., u = (x0 - x, y0 - y). O seu comprimento pode ser obtido através do |u| (módulo de u), que se escreve assim, |u|² = (x - x0)² + ( y - y0)², ou

                                              

Além disso um vetor u por exemplo, pode ter seu tamanho reduzido ou ampliado através de um t qualquer pertencente a os Reais. Se t < 1, teremos uma redução, se t > 1, teremos um ampliação. Se t < 0. teremos uma mudança de sentido, isto é, o se o vetor u aponta para a direita, depois de multiplicado por esse t, ele inverte o seu sentido mudando para a esquerda. Essa mudança pode ser maior do que o vetor u original ou menor que ela, com t > -1 ou t < -1, respectivamente. Se t = 1 ou t = -1 não houve mudanças no tamanho. 

Fig. 2.1.2: Vetor tu, com t > 1. Observa-se que nesse caso o vetor u teve um aumento de t vezes o seu tamanho

OBS: Um caso interessante

Quando, dado dois vetores, um é perpendicular ao outro, o produto interno entre ambos é zero, ou seja um número real. Seja u, v vetores tal que u.v = 0. Sendo u = (a, b) e v = (c, d), temos:

u.v = ac + bd = 0

Por exemplo. Os vetores x = (1,0) e y = (0,1), são, na verdade, os eixos "x" e "y" do plano do R². Veja que o eixo x = (x, 0), pois dados dois pontos de x, seja O = (0,0) e B = (x, 0), temos que o vetor x = B - O:

x = (x, 0) - (0,0)

x = (x, 0)

 De modo análogo temos que e y = (0, y), pois sendo O = (0,0), C = (0, y), pontos de y, temos que y = C - O, ou seja

y = (0, y) - (0, 0)

y = (0, y)

Dando um tamanho inicial a eles, seja x = 1 e y = 1 unidade qualquer, temos x = (1,0) e y = (0,1). Então:

x.y = (1, 0).(0. 1)

x.y = 0 + 0

                            x.y = 0.                       (i)

Logo os eixos "x" e "y" são perpendiculares entre si.

2.2 ÂNGULOS ENTRE VETORES

Dados dois vetores u, v não nulos e não colineares, isto é, um não é múltiplo do outro, podemos identificar um ângulo β entre eles. Comecemos falando da desigualdade Cauchy Schwarz .

2.2.1 Desigualdade Cauchy Schwarz 

Seja u, v vetores não nulos. Para qualquer α ϵ R, temos:

(u + αv)(u + αv) ≥ 0

Efetuando o produto escalar:

u.u + u(αv) + u.(αv) + α²(v.v) ≥ 0

α²|v|² + 2α(u.v) +|u|² ≥ 0

É fácil observar que temos aqui uma equação de grau II em função de α. Como α² > 0 e u, v ≠ 0, calculando o ∆ da equação de II grau, fica:

∆ = b² - 4ac ≤ 0

(2u.v)² - 4|v|².|u|² ≤ 0

4(u.v)² - 4|v|².|u|² ≤ 0

(u.v)² ≤ |v|².|u|²

Considerando u.v > 0, temos:

|u.v| ≤ |u|.|v|       ( I )

2.2.2 Usando o cosseno para encontrar o ângulo entre dois vetores. Ver figura 2.2.1

Pela equação (I), temos:

  |u.v|    ≤ 1  =>          | |u.v|   | ≤ 1

|u|.|v|                        | |u|.|v||

  -1 ≤ | |u.v|   | ≤ 1. Como temos  0 ≤ β ≥ π, fica

           | |u|.|v||

cosβ =    u.v           (II)

           |u|.|v|

Fig. 2.2.1.: Os  vetores u e v em ângulo beta.

2.2.3 Provando (i)

De posse de (II), podemos encontrar qualquer ângulo entre dois vetores. Provemos, por exemplo, (i):

Como o eixo "x" (abcissas) faz 90° com o eixo "y", temos:

COS(90°) =     x.y    

                     |x||y|

x.y = |x|.|y|.cos90°

x.y = |x|.|y|.0

x.y = 0

Como queríamos demonstrar 

2.3 PRODUTO VETORIAL

Dados dois vetores, u e v podemos determinar um vetor  w tal que u e v seja perpendicular a w. Logo temos que  u.w = 0 e v.w = o. Ver figura 2.3

Fig.2.3. : Vetores u., v perpendiculares ao vetor w.

Seja u = (a. b, c), v = (d, e, f) e w = (x, y, z). Como u.w = 0 e v.w = 0, temos:

(a, b, c).(x, y, z) = 0 e (d, e, f).(x, y, z) = 0

ax + by + cz = 0

dx + ey + fz = 0

Então, como possível solução:

x = bf - ec

y = dc - af

z = ae - db

Fica:

w = ( bf - ec,  dc - af, ae - db) (III)

Logo w é o produto vetorial de u por v e se escreve assim: u x v.

Na observação do item 2.1, vimos que podemos escrever os eixos "x" e "y" como (1, 0) e (0, 1). De forma análoga a apresentada em 2.1 escrevemos o eixos em R³ como x = (1, 0, 0), y = (0, 1, 0) e z = (0, 0, 1). Chamando de i, j e k respectivamente x, y e z a combinação linear entre tais eixos resultam no total espaço R³.

Seja (x, y, z) ϵ R³. Então:

(x, y, z ) = x(1, 0, 0) + y(0, 1, 0) +z(0, 0, 1)

(x, y, z) = xi  yj + zk. 

Para memorizar tratemos a combinação linear acima como um determinante de terceira ordem:

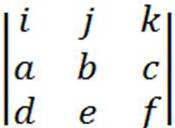
Resolvendo o determinante, temos:

= ( bf - ec)i - (af - dc)j +  (ae - db)k

= (bf - ec, dc - af, ae - db), como em (III)

3. DISTÂNCIA ENTRE DOIS PONTOS

Seja o eixo OXYZ  a seguir:

Fig. 3. : Representação da distância PQ

Pela Fig. 3, observamos a distancia do ponto P ao ponto Q. Veja que por Pitágoras, temos as seguintes relações:

PQ² = SP² + SQ²  ( * )

SQ = (z - z0)

PS = P0Q0

(P0Q0)² = HP0 + HQ0 

(P0Q0)² = (x - x0)² + (y - y0)²

PS² = (x - x0)² + (y - y0)²

Em ( * ), vem:

PQ² =  (x - x0)² + (y - y0)² +  (z - z0)². Logo: 

4. EQUAÇÃO PARAMÉTRICA DA RETA

Claro que falando de distâncias vem logo à mente as retas. E como seriam as equações das retas no R³? Bom, podemos obtê-las de uma maneira mais bem geral que no R². Mais uma vez vamos apelar para uma figura para entendermos melhor coo funciona.

Fig. 4: Reta r paralela ao vetor v

Pela Fig.4, um ponto P(x, y, z) pertence a r se AP = tv, para t ϵ R. Veja que AP é o vetor v, ou alguns de seus múltiplos, deslocado. Seja A(x0, y0, z0) e v = (a, b, c). OBS.: Não confundir A e P, que são pontos, como v, que é o vetor.

Temos AP = (x - x0, y - y0, z - z0).

Como sabemos que AP = tv, fazemos:

(x - x0, y - y0, z - z0) = t(a, b, c)

Veja que:

x = x0 + at

y = y0 + bt }   ==> r          (**)

z = z0 + ct

Que é a equação paramétrica da reta.

4.1 Exemplo.

Encontre um ponto pertencente à reta que contém o ponto A(2, 1, -3) e é paralela a os vetores v = (3, -2, 2).

#RESOLUÇÃO

Por (**), temos que:

x = 2 + 3t

y = 1 - 2t    } ==> r

z = -3 + 2t

Como t é qualquer real, atribuímos um valor a t. Seja t = 1. Então fica:

     x = 5

r: {y = -1

     z = -1

5. PLANO

O R³ guarda fascinantes objetos matemáticos, como por exemplo o plano interagindo com outros elementos. O que seria então esse plano? Como o próprio nome já diz, podemos obter um plano a partir de pelo menos dois vetores, mas precisamos de pelo menos três para encontrar sua equação. Algebricamente falando se os vetores u, v e w não são múltiplos entre si acabam gerando o R³, i.e, (x, y, z) ϵ R³ => (x, y, z) = . u + v + w. Veja que (x, y, z) = a(x, 0, 0) + b(0, y, 0) + c(0, 0, z) com a = b = c = 1 e a, b e c ϵ  R.

5.1 Equação do Plano

Mais uma vez recorramos a uma figura para entender melhor o que se segue. Ver figura 5.

FIG. 5: Plano  π  

Seja A(x0, y0, z0), B(x, y, z) e o vetor n = (a, b, c). Temos:

u = B - A = > u = (x - x0, y - y0, z - z0)

Como u ┴ n:

n.u = 0


(a, b, c)(x - x0, y - y0, z - z0) = 0

ax + by + cz - ax0 - by0 - cz0 = 0

Fazendo a expressão em negrito igual a d, ou seja, d = - ax0 - by0 - cz0, fica:

ax + by + cz + d = 0. Logo 

Equação Geral do Plano

π: ax + by + cz + d = 0

Se dois Planos se interceptam o resultado será uma reta.

5.2 Equação Paramétrica do Plano

Fica ao leitor tentar deduzir a Equação Paramétrica do Plano. Usando os conceitos de definição de vetor e de retas é possível obter o resultado.

6. CONCLUSÃO

Não se pretendeu de maneira aqui esgotar o assunto. Na verdade muitas coisas foram omitidas ao leitor, como algumas provas e demonstrações mais rigorosas. Doravante é essencial agora que se ponha em prática o exposto resolvendo muitas atividades. Espero poder ter ajudado um pouco no entendimento.

Se alguma coisa ficou obscura, não clara ou algum possível erro, por favor, não exite em me comunicar, pois estarei de prontidão e honrado em corrigir.

7. REFERÊNCIAS

REIS, Genésio Lima dos; SILVA, Valdir Vilmar da. GEOMETRIA ANALÍTICA. Rio de Janeiro: LTC, 1984.

LIMA, Elon Lages. Álgebra Linear. Rio de Janeiro: IMPA, 2011. (Coleção Matemática Universitária)

LIPSCHUTZ, Seymour. Álgebra Linear - Teorias e Problema. São Paulo: Perason Makron Books, 1994. (Coleção Schaum)