Do grego "triângulo mais metron (medida)" a trigonometria é um ramo da matemática que estuda os triângulos e suas razões com os ângulos. Sua utilidade é vasta e sem dúvida é uma das mais requisitadas e estudadas áreas da matemática pelo seu grande número de serventias à outros campos.
Uma forma bastante fácil de se compreender a Trigonometria é a partir do triângulo Retângulo, ao qual possibilita trabalhar com alguns ângulos. Dele podemos suscitar hipóteses e conclusões que auxiliarão em muito a compreensão não só da sua relação com a geometria, mas também com as funções.
RELAÇÕES TRIGONOMÉTRICAS NO TRIÂNGULO RETÂNGULO
Quando se fala em trigonometria certamente também se está falando em ângulos. Uma forma prática de se conhecer as relações que existem entre eles é a partir de suas razões: seno, cosseno, tangente, cotangente, secante e cossecante.
* SENO
Diz-se que o seno de um ângulo é a razão entre o cateto oposto de uma triângulo retângulo por sua hipotenusa.
Seja o triângulo retângulo ABC, de lados a, b, c com hipotenusa a abaixo:
Figura 1: Triângulo Retângulo ABC e sua relação com o seno
* COSSENO
O cosseno de um ângulo é a razão entre seu cateto adjacente por sua hipotenusa. Este processo é análogo ao anterior. Seja o triângulo retângulo ABC, de lados a, b, c com hipotenusa a abaixo:
Figura 2: Triângulo Retângulo ABC e sua relação com o cosseno
*TANGENTE
A tangente é a relação entre o seno e o cosseno de um determinado ângulo, ou ainda pode ser definida como a razão entre o cateto oposto de um ângulo pelo seu cateto adjacente. Análogo à figura anterior, fazemos:
A tangente é a relação entre o seno e o cosseno de um determinado ângulo, ou ainda pode ser definida como a razão entre o cateto oposto de um ângulo pelo seu cateto adjacente. Análogo à figura anterior, fazemos:
O restante das relações, como cotagente, secante e cossecante serão oruindas das já vistas figuras 1 e 2.
* COTANGENTE
A cotangente mostra-se ser a razão entre o cosseno de um dado ângulo pelos seu seno, sendo, portanto, o inverso da tangente. Pode ser escrita assim:
* SECANTE
A secante é o inversa do cosseno, isto é,
* COSSECANTE
A cossecante é o inverso do seno, assim:
ÂNGULOS NOTÁVEIS
Existem alguns ângulos que são notáveis, isto é, se destacam dentro da gama de 360 ângulos que há. São eles, 30º, 45º e 60°, com seus respectivos múltiplos, ou côngruos com pequenas variações nos sinais, a depender de que quadrante se encaixam. Não está entendendo que história é essa de quadrante? Não se preocupe, aqui mostraremos do que se trata, mas antes vamos às relações que demonstram como surgiu os seno e cosseno desses ângulos. Vê-se que claramente não é preciso se calcular os valores da tangente, cotagente, secante e cossecante, umas vez que essas razões dependem apenas do seno e cosseno.
ÂNGULO DE 30°
Seja um triângulo eqüilátero de lados a, b e c, iguais, conforme figura abaixo. Por definição sabe-se que
a = b = c. Dividindo esse triângulo ao meio numa altura h, um dos ângulos resultantes será 30º e os outros 60 º e 90º.
a = b = c. Dividindo esse triângulo ao meio numa altura h, um dos ângulos resultantes será 30º e os outros 60 º e 90º.
Figura3: Triângulo equilátero
Seno
Como o sen30º = b/2/a, e b = a, fica:
Cosseno
Como cos30º = h/a, é necessário encontrar o valor de h:
Por Pitágoras temos:
Donde,
Tangente
A tangente pode ser obtida como o quociente entre sen30º/cos30º, ou na razão entre o cateto oposto pelo cateto adjacente, isto é, tg30° = a/2/h, donde,
Cotangente
A cotangete pode ser obtida através da razão inversa da tangente, isto é, cot30º = 1/tg30º, assim:

Secante
A secante consiste na razão inversa do cosseno, isto é, cosc30° = 1/cos30°. Fica:
Cossecante
O cossecante é a razão inversa do seno, isto é, cosc30° = 1/sen30°, assim:
Por processo análogo, encontramos os seno, cosseno, tangente, cotangente, secante e cossecante de 45°e 60° ou quaisquer outros graus, notáveis ou não. Deve-se colocar uma observação no ângulo de 45° que deverá ser demonstrado por outro tipo de triângulo distinto do da figura 3. Neste caso seria mais expressivo usar um triângulo retângulo isósceles, já que possui dois lados iguais e dois ângulos de 45°.
ANGULO DE 45°
Seja um triângulo isósceles com b = c ,abaixo, :
Sabemos que:
O sen45° = c/a <=> b/a, a o que obtemos:
O seno de 45° é justamente igual a o seu cosseno já que os catetos oposto e adjacente são iguais, isto é:
Tangente
A tangente pode ser obtida como a razão entre o cateto posto e o cateto adjacente, isto é, tg45° = b/b => 1 ou pelo quociente entre o sen45° e o cos45°, assim:
Cotangente
Cotg45° = 1/tg45°
Cotg45° = 1
Secante
Sec45° = 1/cos45°, ou seja:
Cossecante
Cosc45° = 1/sen45°,donde resultará no mesmo valor anterior da secante, isto é:
As demais demonstrações angulares ficam a cargo do leitor que poderá fazê-lo como exercício do exposto aqui.
Todas as razões apresentadas anterioremente também tem comportamentos distintos quando inseridos nos gráficos constituindo-se, portanto, funções trigonométricas. Cada função tem um campo definido de seu domínio e a depender do sentido de rotação podem ser positivos ou negativos.
FUNÇÕES TRIGONOMÉTRICAS
Ainda em construção...










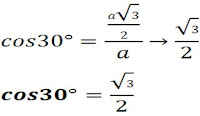










4 comentários:
parabéns foi de bom uso o seu entendimento
Seus animais, tangente de 30 é raiz(3)/3
e não raiz(3), que no caso é a de 60
Acredito que a imagem cortou o raiz de 3 sobre 3.
Foda-se tudo!
Postar um comentário