A Geometria Não Euclidiana e as Barreiras da Matemática

Calculando o Infinito

A Integral

Ao longo dos séculos o homem sentiu necessidades imperiosas da obtenção do valor exato, ou pelo menos aproximado, de algumas áreas e/ou volumes de certas figuras geométricas com  contornos irregulares. Ele já sabia calcular áreas e volumes de figuras regulares, como cones, pirâmides, cubos, prismas, esferas entre outros, não obstante outros tipos de figuras continuavam sem esclarecimento.

Com a chegada de Isaac Newton e Leibniz essa história começou a ser contada de um novo capítulo, com a introdução do Cálculo Diferencial e Integral.

Aqui nos concentraremos em demosntrar a definição técnica da Integral não contendo, porém, os principais meios de resolução destas, que será mais bem tratado em outro artigo.

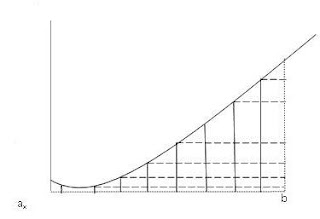
Basicamente esse cálculo consiste no estudo de uma dada função f(x) definida no intervalo [a, b], conforme figura a seguir:

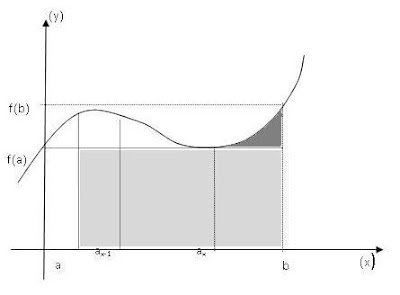
A idéia é de obter a área da região hachurada da figura ao lado. 

Como pode ser observado uma parte da área, a de cor mais fraca, forma um retângulo que pode ser calculado através de (b - a)(f(a) - 0), contudo ainda resta a parte da área compreendida entre f(b) e f(a), com mesmo domínio fechado de [ax, b]. A parte de cor mais forte tem contornos irregulares que tornam seu cálculo muito complicado. Como então obter seu valor exato?

Dividindo-se o gráfico em pequenas partes é possível obter a área dessas pequenas partes divididas, assim:

É o somatório dos pequenos retângulos em escalas cada vez menores que definirá o valor da área final. É perceptível que quanto mais se quebre o gráfico em pequenos gráficos e o amplie, cada vez mais retângulos e áreas semehantas à de cor mais forte do primeiro gráfico vão se gerando, e assim até o infinito. Há um ramo dentro da matemática capaz de determinar valores que tendem ao infinito e é através do estudo de Limites.

Assim sendo podemos dizer que uma Integral é definida por:

Esta última notação da equação acima é como se escreve, matematicamente, uma integral, que significa literalmente somar partes, seja para áreas, volumes ou quaisquer cálculos que requeiram somatórios.

Bom como já visto é preciso que a função seja definida no irtevalo fechado [a, b] e que seja contínua. Uma vez tendo esses atributos o próximo passo é verificar que tipo de função se está usando e é aí que está o problema: Existem diversas maneiras de se trabalhar com integrais e cada uma deleas requer um tipo de especial de resolução ou estratégia.

TIPOS DE INTEGRAIS

Existem as Integrais Definidas, que são como essas estudadas anteriormente em que é preciso os valores dos limites do domínio ou da imagem da função, e também as Integrais Indefinidas, que não precisam de um intervalo fechado. Ora, essa última serve mesmo apenas de conhecimento teórico uma vez que sem um intervalo não é possível se calcular com precisão nada. Em exercícios é comum o uso desses tipos de Integrais, mas para o uso devido na vida prática é preciso a existência do intervalo.

Há ainda as Integrais resolvidas por Substituição, as Parciais, Polares, por Partes, entre outras. Estamos falando aqui dos tipos de resoluções dessa poderosa arma da matemática que será tratado em breve aqui.



CURIOSIDADE
PRATO DO DIA: PLANETA ASSADO

Plantas carnívoras, animais canibais, guerra por alimento. Tudo isso parece ser imensamente terráqueo, mas quem pensa que é só na Terra que há matanças está enganado.

A imagem abaixo ilustra o apetite voraz de uma estrela que rouba, a cada tempo que se passa, mais e mais gás de um planeta em sua órbita pois o dito cujo se trata de um corpo gasoso que só não é classificado como estrela por não possuir massa suficiente para as mesmas, mas que possui temperautra semelhante a o de uma pequena estrela fria.

Créditos da Imagem: (BARBOSA, Cássio, Jornal G1- Globo)

Com futuro bem perto das entranhas dessa estrela, o nosso planeta acima figurado tem seus dias contados até sua digestão. O interessante é que fatos como esse não são raros no Universo. Há diversos tipos de exemplos de não só estrelas engolindo planetas, mas também de estrelas engolindo estrelas, galáxias engolindo galáxias e até nmesmo aglomerados de galáxias inteiras sendo comidas por outras galáxias. Canibalismo até no espaço!

O Grande Enigma de Fermat: O Última Teorema

Um prêmio milionário oferecido para conquista, uma mulher disfarçada de homem com única forma de dar andamento aos seus trabalhos, as maiores mentes do planeta sendo enganadas facilmente sendo necessário a fusão das mais modernas técnicas e inteligência já inventada antes para um longo mistério que atravessou a barreira temporal de mais de 350 anos sem solução, e como artista principal de todo o enigma mais famoso da história da Matemática um homem tido amador: Estamos falando sobre o Último Teorema de Fermat, o maior e mais famoso mistério matemático dos últimos séculos sendo desvendado somente em 1994 por uma mente não menos prodigiosa que as demais, levando 7 anos da vida de um homem.  


  "Descobri uma demonstração maravilhosa desta proposição que, no entanto, não cabe nas margens deste livro." (Aczel, 1997)

O Último Teorema, como é carinhosamente chamado o enigma proposto por Fermat, nasceu de uma  curiosidade deste ao manipular a bela equação pitagórica x² + y² = z². Encontrando fácil inúmeros valores como solução do problema, em um estalo de genialidade resolve mudar o expoente 2, para 3, na forma de x³ + y³ = z³ e o que encontra? Uma bela e misteriosa surpresa: Não percebeu nenhuma solução para o que acaba de criar, e mais, aumentando ainda o expoente n vezes fez crescer e nascer um enigma que perturbaria as maiores mentes matemáticas de todos os tempos.

Na margem do dito livro teria escrito:

"É impossível para um cubo ser escrito como a soma de dois cubos ou uma quarta potência ser escrita como a soma de duas quartas potências ou, em geral, para qualquer número que é uma potência maior do que a segunda, ser escrito como a soma de duas potências com o mesmo expoente."  (Singh, 1998, p. 82)

ATÉ EULER CAIU
Leonard Euler é conhecido como um dos "Príncipes da Matemática" e junto com Gauss também não consegiu desvendar o problema. Encontrou solução para os casos em que n = 3, mas não obteve sucesso em uma generalização de n pertencente ao conjunto dos Números Naturais.  Euler é famoso por sua proezas nos campos da Análise, Cálculo, Álgebra, reiventou boa parte do linguajá matemático e criou Teorias e demonstrações de Teoremas dignos de nota, sem falar nos mais de 800 artigos que fazia por ano e que até hoje muitos deles ainda estão sendo publicados pela Universidade de São Petersburgo, local onde trabalhou por muito tempo. Argand Gauss, ou por frustação de não ter encontrado uma solução, ou mesmo por ser verdade, argumentou que não tinha interesse na demonstração da prova do problema e que portanto não a faria. Outros matemáticos em todo o mundo continuaram incansavelmente pela busca de uma demonstração, muitos foram os que colocaram em disponibilidade várias "soluções", mas todas não passavam quando eram submetidas a exames minunciosos e rigorosos.


O GRANDE ENIGMA RESOLVIDO
Somente após o nascimento de um gênio que o grande mistério pode ser resolvido.
Ao visitar a Biblioteca de sua cidade, um jovem inglês, ainda criança, se apaixounou por um livro que argumentava sobre uma dor de cabeça que perseguia os matemáticos em quase 4 séculos, e era o Teorema de Fermat. O que mais deixa picante o tal do problema é que o mesmo Fermat diz tê-lo resolvido, mas que pelo pouco espaço nas margens do livro onde fazia anotações não pode completá-lo e deixou para um mundo o desafio de quem também o provasse. O jovem curioso a essa hora de leitura já estava sabendo disso e naquele instante nascia a vontade de um homem.
Apenas mais tarde, já graduado, é que Andrew Wiles, trabalhando para a Universidade de Princeton, Estados Unidos, encontrou a solução para o mistrioso problemas que atravessara séculos.

O matemático levou 7 anos de sua vida, sendo que parte desses anos ainda teve que corrigir uma pequena falha nos argumentos, o que levou a uma correção de 200 páginas. Em 1994 estava resolvido e derootado um dos maiores desafios matemáticos do mundo por um até então sonhador que crescera, tornara-se matemático e um dos poucos a compor a pomposa galeria dos grandes matemáticos.

A Natureza Musical nas Obras Matemáticas

Mozart, Beethoven, Bach, Vivaldi entre outros tantos compositores enriquecem a alma humana com suas lindas obras musicais. Entretanto uma bela canção começa mesmo com uma boa matemática. As notas musicais, seus tempos e escala obdecem regras matemáticas muito bem definidas e que auxiliam no processo criativo e memorizável delas. Quem diria que podem escrever música? Como escrever algo que simplesmente se ouve? Parece, à primeira vista, difícil de se conceber, mas é justamente o que ocorre com as chamadas partituras.

Mais além ainda  vai o imaginário humano: Compondo  ele trancede a nobre capacidade de apenas nascer, crescer, se "desenvolver", envelhecer e morrer. Ela recria um sentimento que se concebe dentro da alma, vai crescendo e assumi um papel totalmente fora da vidinha que muitos têm por aí, ele sabe, neste momento, que viver é uma arte e viver bem, a mais bela das artes e que esta pode ser conhecida mediante uma bela cançao ouvida e tocada!

A construção das músicas são mais complexas do que se pode supor com uma pequena observada. Embora muitos tenham talento nato para criar e recriar, há tanto nas melodias ainda por se descobrir que se torna inesgotável as possibilidades de mais criações. Se valendo disso muitos matemáticos ao longo da história se beneficiaram do teor musical para inspirarem-se em suas obras, isto é, em suas descobertas numéricas. Um deles foi o grande físico Abert Einstein que amava tocar e ouvir violinos entre outros instrumentos de música clássica. Também vale destacar que foi um grande matemático, Pitágoras, um dos pioneiros no estudo dos tempos musicais

Interessnate que os matemáticos dizem que Deus fala por números, mas os músicos dizem que Deus se faz ouvir por músicas e não por palavras, nem muito menos por números. Não obstante o que se observa é que ambas áreas do cohecimento, apesar de possuirem definições distintas, por muitas vezes esbarram em algo incomum. Em outras palavras a música constituir-se-ia numa forma musical de números, ou a matemática numa forma numérica musical. O fato é que a Teoria dos Números e dos Conjuntos Numéricos auxiliam os músicos no entendimento de sua arte; sequencias como a de Fibonacci são intrínsecas e a Razão Divina também encanta os criadores de melodias. De fato esta é abstrata, mas nada é tão abstrato quanto à própria matemática, afinal de contas ela é concebida no ventre do cérebro de alguém e provoca tamanho prazer e bem estar quanto a qualquer beijo ou sensação agradável. 

Há uma razão para existir ambas as ciências - Matemática e Música - talvez para explicar o funcionamento do Universo, quiçá desvendar os mistérios do cérebro, ou também apenas simplesmente deixar a vida dos mortais humanos com mais sentido e agradável de se viver!

Escuta aí essa bela Canção, o Canon

Coordenadas Polares - O que são?

Muito usadas no Ensino Superior, as Coordenadas Polares ainda são pouco conhecidas, principalmente no Ensino Médio, e menos ainda suas aplicações.

Bom, comecemos por dizer o que são coordenadas Polares:

Como o próprio nome já diz são um tipo de notação de coordenadas que se colocam num plano bidimensional, como um tipo especial de plano semelhante ao Cartesiano, só que utiliza outros parâmentros. Usando uma definição mais matemática, poder-se-ia dizer que é um plano de coordenadas (r, θ),sendo r = raio e θ = a um ângulo qualquer, aplicadas sobre um plano, conhecido com pólo (origem) equivalenmte ao eixo x nas coordandas cartesianas. Uma vez escolhido o raio que se quer, traça-se na direção do ângulo θ uma semi-reta (raio), assim:

Figura 1.a: Representação de coordenada polar no plano

Ora, para plotar uma determinada coordenada basta inserir seus valores nos respectivos eixos, isto é, seja a seguinte coordenada (1, π/3), no gráfico ela fica:

Figura 1.b: Par ordenado (1, π/3) em coordenadas polares 

OBS: É importante verificar em qual notação está se usando os valores para θ. Normalmente utiliza-se a notação em radianos, isto é, ao invés de dizer que um ângulo tem 60º, diz-se que ele tem π/3rad, que é o seu correspondente em radianos.


Esse intricado sistema foi desenvolvido por Isaac Newton para facilitar alguns cálculos matemáticos. Apesar de ainda não ser amplamente conhecido o sistema oferece uma nova abordagem sobre gráficos e funções apresentando contornos curiosos. Por exemplo, veja plotagem da função r = 1 + senθ

Figura 2: Crardióide

De modo análogo ao que ocorre nas coordenadas cartesianas, em que se atribuem valores à funções para se obter o gráfico, também o é em coordenadas polares. Observemos abaixo alguns valores

θ        r = 1 + senθ                        (r, θ)

0        r = 1 + sen0                         (1, 0)
π/6     r = 1 + senπ/6 => 1 + 1/2     (3/2, π/6)
π/4     r = 1 + senπ/4 => 1 + √2/2   (1 + √2/2, π/4)

π/3     r = 1 + senπ/3 => 1+√3/2     (1 + √3/2, π/3)
π/2     r = 1 + senπ/2 => 1 + 1        (2, π/2)
.
.
.
E assim sucessivamente. Uma vez encontrados os valores é só plotar, como no exemlo anterior e juntar os pontos. Foi dessa forma que nasceu a nossa bela Cardióide acima, nome esse dado por assemelhar-se a um coração.

Por exemlo podemos calular uma rosa de n pétalas. Seja r = 1 - 3cos(10θ), o resultado será uma rosa de 20 pétalas, veja:

Figura 3: Rosácea de 20 pétalas

Essa plotagem torna-se muito trabalhosa se feita na mão bruta, então é melhor usar programas que desempenhem funções matemáticas mais complicadas, como na imagem acima. Neste caso foi utilizado o programa Wimplot, mas há dezenas de outros que tem a mesma finalidade. Com o uso desses programas é possível inventar uma infinidade de gráficos de diversos tipos, fazer comparações, estudar sinais, derivadas, áreas, volumes, comprimentos entre outros cálculos.

Uma pergunta naturalmente surge: E se fosse em coordenadas cartesianas, como ficariam essas coordenadas?
Para responder a essa pergunta é necessário irmos para o plano. Seja o plano abaixo

Figura 4: Coordenada polar (r, θ)

Pela relação trigonométrica sabemos que

senθ = x´M´/r (Equação I)

cosθ = ox´/r     (Equação II)

Donde

x´M´= y    
e

ox´= x, onde x e y é o par ordenado, (x, y).

Substituindo nas equações I e II, temos:

senθ = y/r => y = rsenθ

cosθ = x/r => x = rcosθ 

Por Pitágoras fica:

r² = x² + y²

Que são as respectivas fórmulas para se transformar coordenadas polares em cartesinas e vice-versa.

Seja o par ordenado (1, π/3) da figura 2, podemos transformá-la em coordenadas polares aplicarndo as fórmulas descritas acima, assim

y = 1sen(π/3)

y =  √3/2

e

x = 1cos(π/3)

x = 1/2

Então fica (1/2, √3/2)

No gráfico fica:

Figura 5: Gráfico Cartesiano

Por fim no Winplot podemos vislumbrar lindas figuras como a seguir

Figura 6: Várias funções na construção dos gráficos

Certamente criações como estas revelam quão linda e fascinante é o mundo da matemática. Além das coordenadas polares existem as coordenadas implícitas, explícitas e paramétricas no plano bidimensional (x, y) adicionadas às esféricas e cilidnricas no tridimensional (x, y, z).

A Equação de Brizola

Assembléia Legislativa lotada. Nela há deputados de todos os níveis discutindo, mais uma vez, o destino e as regras da sociedade através de Portarias, Decretos e Leis. Numa delas um impasse: Um terrível conflito de votos e a dúvida de um suposto empate, colocando um voto, o do desempate, nas mãos de um Sistema de Equação do I grau. Mentira? História hipotética? Não, foi justamente isso que ocorreu na Assembleia Legilstaiva de Porto Alegre, RS.

Num gesto inédito na política brasileira, o Deputado Leonel Brizola, utiliza-se de dotes matemáticos para resolver um conflito de idéias.

Tudo começou quando foi rejeitado, pela mesa julgadora do Rio Grande do Sul, o provimento do cargo de Vice-Governador através de voto indireto por 36 votos a 15. Ora, se arranjando no art. 249, em seu parágrafo 3^o, da Constituição do Estado (Rio Grande do Sul), Leonel Brizola argumenta que a decisão fora ilegal, uma vez que pela mesma Lei acima descrita, era preciso 2/3 dos votos para sagra-se legal. Sabendo que havia 55 Deputados, sendo que o do Presidente da Mesa só é usado em questões de desempate, o então Deputado Trabalhista Leonel Brizola, argui que ocorrera, de fato, um empate. Como assim, não foram 36 votos a 15?

Bem se analizado criteriozamente pelo leitor, 2/3 dos 55 votos totais são em torno de 36, 66... sabendo que seria "impossível" haver empate numa ordem fracionária de 2/3 os outros Deputados naturalmente discordaram do nobre colega, o que obrigou-o a utilizar-se de um poderoso artifício matemático. 

"Convenhamos, porém que apenas 54 deputados votam efetivamente em plenário pois que o Senhor Presidente cabe o voto de desempate, ou mais precisamente, o Senhor Presidente deve votar apenas quando o seu voto for decisivo. Ora sob a base do critério dos dois terços, quando deveria caber o voto de desempate? Respondo: Precisamente quando se verificar em plenário o resultado 36 x 18. E ainda toda vez que um dos grupos obtenha 36 votos, o número de votos do outro poderá variar desde 0 até 18, e para qualquer valor (entre tais limites) ainda haverá empate, desde que se tenha em vista que um único voto poderá alterar decisivamente a votação. Portanto, o voto emanado da cadeira presidencial, tal como para o critério da maioria absoluta – 27 x 27 – é decisivo e, indubitavelmente, de desempate. Pois se o Senhor Presidente, manifestar-se favorável, ao grupo dos 36, este alcançará maioria de dois terços" Disse Brizola.

O que o nobre Deputado queria dizer é que era possível ocorrer sim o empate no critério de 2/3, como rezava a mencionada Lei Estadual, e mais, que os 36 votos não eram suficientes para a vitória. Então, a fim de provar o que dizia, fez do seguinte dote matemático, em suas palavras:

"Considerando que a Assembléia compõe-se de 55 membros e que apenas 54, como afirmei, votam efetivamente em plenário, será fácil demonstrar em que condições deverá ocorrer o empate, dentro do critério de dois terços. Chamemos de x o número de votantes do grupo maior e y o número componente do grupo menor, grupos que somados deverá perfazer 54. Ora, para que ocorra um empate, deveremos ter:

obtemos, desse modo, uma equação com duas incógnitas. Sabemos que a soma das incógnitas x+y é igual a 54. Podemos pois escrever o seguinte sistema:

	x + y = 54

que resolvido nos dá:

x = 36
y = 18

Pela equação cima descrita, o Deputado usou a matemática como uma poderosa argumentação de sua tese, para isso era preciso que os 2/3 = 1/3, o que somados dão 1 inteiro, pois 1/3 + 2/3 = 1, isto é, a os votos da Assembléia inteira. Como a maioria figurava "X" e a minoria "Y", dever-se-ia encontrar algo que provasse que a maioria era igual a minoria, por isso 1x/3 = 2y/3. Como o total deveria ficar nos 54 votos, pois segundo o nobre Deputado o último e decisivo voto deveria ficar com o Presidente, o total de x + y, isto é, a maioria + a minoria, deveria ser igual a 54, assim havendo empate a este que deveria  a honra do desempate. Como já foi visto no resultado do Sistema de Equação, x = 36 < 36,666... e y = 18, ocorrera, de fato, um empate. Como assim? Se substituir 36 na equação de "x" e 18 na equação de "y", verificar-se-á que há, de fato, um empate.

REFERÊNCIAS BIBLIOGRÁFICAS

 MATEMÁTIVA HOJE - CURIOSIDADES. Disponível no site:http://www.matematicahoje.com.br/telas/cultura/curiosidades/curiosidades.asp?aux=J . Acesso: 1 de jan. de 2010. 

Clique aqui para ir ao site que originou este artigo.

ANÁLISE CRÍTICA

Bom é preciso muita cautela para compreender matematicamente a idéia do raciocínio de Brizola. De fato notável argumentação, mas toatlmente tendencionista. O que fez o nobre político foi manobras matemáticas que o apoiassem em sua tese. Valendo-se de uma possível ignorância  matemática dos Deputados  ali presentes, pois este era enhenheiro, utilizou-se de um sofisma, isto é, uma prova matemática aparentemente rigorosa, mas que na verdade contém erros crassos. Neste caso o erro não consite no cálculo, mas ao raciocínio que leva a isso.

Quando ele fala em maioria, pode prestar atenção o leitor, que usa o termo "x" para tal demonstração, mas o "x" fica com os 1/3, que é a menor parte, não a maior. Outra manipulação foi a igualdade. Não é possível que 1/3 seja igual a 2/3, pois ambas utilizam-se da mesma variável "x", sendo desnecessário o uso de duas variáveis, "x" e "y". O "y" fora colocado para mascarar a variável que era uma só, no caso o "x". Em outras palvras, o que estva em jogo eram os votos. Se "x" fosse a maioria deveria ter sido colocado em 2/3 e "y" em 1/3. A única razão que ele tinha era que os 2/3 não haviam sido alcançados, o que de fato é de fácil comprovação matemática.

Porém um empate era pedir de mais, mas utilizar-se de matemática nas questões parlamentares, políticas e quaisquer que sejam é plausível, afinal de contas é para isso que serve a matemática, para resolver questões de interesse cotifdiano ou não. Uma solução gráfica é atendida, mas o dados desta estariam incorretos. Pelo raciocínio empregado, qualquer que fosse o número "n"de Deputados ele utilizar-se-ia de uma sofisma ou até mesmo uma solução real, para a dada questão, pois ele igualaria a partes fracionária e claro pelo Sistema de Equações encontraria algum tipo de solução. Nada mal para ser tratado numa Câmara de Deputados onde um raciocínio matemático dessa estirpe necessitaria de um dado tempo de uma maioria que possivelmente não foi bem na escola em matemática.

Discordância no argumento aqui apresentado de discordância ao método do Senhor Brizola, por favor postar no comentário. Uma boa discussão certamente enriqueceria bem o tema.

Obrigado!