MATRIZES
Historicamente o estudo das Matrizes era apenas uma sombra dos Determinantes, linha essa apenas modificada com o surgimento de Joseph Sylvester, primeiro a dar um nome ao novo ramo da matemática, mas coube a Cayley, amigo de Sylvester, não somente a prova, mas também a demonstração das utilidades das Matrizes em sua obra Memoir on the Theory of Matrizes em1858.
Com um estudo recente de apenas cerca de 150 anos as Matrizes ganharam tamanha importância que não se consegue conceber, hoje, a idéia computadores, engenharia civil, elétrica, mecânica, meteorologia, oceanografia entre outras inúmeras áreas sem o estudo delas. Na verdade seu estudo sistemático começou realmente com Cayley, mas antes dele já havia prósperas pesquisas no assunto, principalmente quando Lagrange utilizou Matrizes no estudo de máximos e mínimos de funções reais de várias variáveis.
Nas escolas ainda se usam o estudo de Matrizes e Determinantes, não obstante esse estudo ainda está longe do ideal, que seria ver na prática as suas aplicações. Em parte o erro se deve a má preparação dos docentes, falta de subsídios na escola, investimentos em linhas de pesquisas Júnior e à carência peculiar de matemática. É fato e relevante também observar que muitos profissionais tentam, da melhor maneira possível os permitida, não apenas repassar o conhecimento, mas como também fazê-lo de uma maneira produtiva incentivando, assim, a novas produções e descobertas.
Aqui está apresentado, de maneira suscita as principais propriedades e regras matriciais de maneira lógica e objetiva com não raro rigor matemático. Além disso, há exemplos de cada uma de suas formalidades e subtítulos bem como, ao final, aplicações cotidianas do seu estudo.
DEFINIÇÃO
Uma matriz é um conjunto de linhas e colunas de elementos numéricos organizadas num retângulo e que possuem certas propriedades matemáticas bem definidas. Em outras palavras, é uma tabela de informações codificadas em números.
Seja a matriz dada abaixoOs elementos matriciais de A podem ser generalizados como Amxn = (aij), onde m e n é a ordem da matriz entre linhas e colunas respectivamente, i o número de linhas e j o número de colunas dos elementos dentro da matriz. Assim se quisermos o elemento da 5ª linha e 6º coluna, o escrevemos assim:
Amxn = (a56)
As matrizes são representadas matematicamente através de parênteses, como em (I), ou através de colchetes. Elas podem ser somadas, subtraídas e multiplicas, possuindo, assim, algumas propriedades. Se forem quadradas possuem duas diagonais, a Diagonal Principal, que parte da esquerda para direita e compreende os elementos do centro, e a Diagonal Secundária, que parte da direita para a esquerda e compreende os elementos do centro no sentido contrário, como a seguir:


SOMA DE MATRIZES
Duas ou mais Matrizes são somadas se, e somente se, suas ordens forem iguais, isto é, Amxn + Bmxn.
Seja a soma das seguintes Matrizes A e B de ordem 2x3 abaixo:
Efetuamos o cálculo obtendo a Matriz C, soma entre os respectivos valores dos elementos de mesma linha e coluna de A e B, assim:
Exemplo 1. Encontre a matriz C soma das matrizes A e B abaixo:
Resolução
A + B = C
Exemplo 2. Por absurdo tentemos somar a matriz A3x2 com a matriz B2x3, que segundo uma das propriedades da adição não é permitida, já que o número de elementos i e j das matrizes não são iguais. Temos:
SUBTRAÇÃO DE MATRIZES
Por processo análogo ao anterior, obtemos a solução.
Exemplo 1. Encontre a matriz C diferença das matrizes A e B abaixo:
Resolução
A - B = C
A partir desse ponto podemos encontrar um tipo de matriz chamada de Matriz Oposta, o que nada mais é do que a troca dos sinais da Matriz B quando essa é negativa, isto é, um pequeno jogo de sinais, assim:
IGUALDADE ENTRE MATRIZES
Por processo semelhante também podemos igualar matrizes. Pegando o mesmo exemplo anterior, suponhamos que saibamos quem é a matriz A e C, mas não a matriz B. Podemos encontrar B da seguinte forma:
A - B = C
Como não sabemos quem é B, fazemos:
Do mesmo modo como somamos e subtraímos, agora igualamos, sempre obedecendo às respectivas linhas e colunas dos elementos matriciais de A e B. Temos:
Encontramos os elementos de B, e como esperado realmente obtivemos uma matriz B2x2
MATRIZ TRANSPOSTA
Seja a matriz
Dizemos que ela pode ser Transposta se seus elementos de linhas e colunas podem se deslocar para colunas e linhas respectivamente e representamos esse tipo de matriz por At, assim:

MULTIPLICAÇÃO DE MATRIZES
Uma matriz
Só pode ser multiplicada por uma matriz B, se e somente se, o número de colunas de A for igual ao número de linhas de B, ou o número de elementos da coluna de A for igual ao número de elementos da linha de B, isto é, se Amxn e Bnxp, cujo produto será Cmxp.
Sejam as matizes do exemplo 2 da SOMA DE MATRIZES descrita anteriormente
Multiplicamos os elementos de mesma ordem da linha da matriz A pelos elementos da coluna da matriz B e os somamos, assim:



Podemos também igualar produtos entre matrizes, desde que obedecidas as propriedades iniciais dadas.
MULTIPLICAÇÃO POR UM ESCALAR K
A mesma Matriz pode ser multiplicada por um valor k qualquer, com k Є R . Seja a matriz A abaixo multiplicada por k, assim temos:
Exemplo 1. Encontra a Matriz 2A abaixo:
PROPRIEDADES BÁSICAS DAS MATRIZES POR ADIÇÃO E MULTIPLICAÇÃO
(i) (A + B) + C = A + (B + C)
(ii) A + 0 = A
(iii) A + (-A) = 0
(iv) A + B = B + A
(v) k(A + B) = kA + Kb
(vi) (k + s)A = kA + as
(vii) 1.A = A
(viii) (ks)A = k(sA)
(ix) 0.A = 0
MATRIZ IDENTIDADE
Uma matriz é dita identidade, e representamos por In, se é quadrada e os elementos de sua Diagonal Principal são todos iguais a 1 e os outros elementos iguais a zero como no exemplo a seguir:
Como a matriz é quadrada escrevemos apenas a notação In;
Exemplo 1. Achar a matriz Identidade I3.

MATRIZ NULA
Dizemos que uma Matriz é nula quando todos os seus elementos são iguais a zero
MATRIZ INVERSA
Dizemos que uma Matriz A é inversa se existe outra Matriz B cujo produto é a Matriz Identidade, onde B = A-1, assim:
A.B-1 = In
A.A-1 = In

MATRIZES QUADRADAS
Algumas Matrizes Quadradas importantes
MATRIZ DIAGONAL
Uma Matriz é dita diagonal se os elementos não-diagonais são todos iguais a zero, isto é;
A matriz Identidade é um exemplo de Matriz Diagonal.
MATRIZ TRIANGLAR
Uma Matriz é dita triangular se os elementos fora as Diagonal Principal são iguais a zero, podendo ser triangulares superiores, se os ditos elementos estiverem abaixo, ou inferiores, se os elementos estiverem acima. Veja:
MATRIZ FAIXA
Chama-se Matriz Faixa aquela que possui todos os elementos da vizinhança da Diagonal Principal iguais a zero, assim:
MATRIZ SIMÉTRICA
Uma Matriz se diz simétrica se AT = A, com A sendo quadrada. Da mesma forma dizemos que uma Matriz A é anti-simétrica se AT = - A
Exemplo 1. Verifique se A é simétrica de B.
Sim a Matriz A é simétrica da Matriz B, pois as linhas de A formam as colunas de B, sendo, portanto, sua Transposta, A = AT
Exemplo 2. Verifique se A é anti-simétrica de B.
Como no exemplo anterior, com B = - A, temos:
MATRIZES ORTOGONAIS
Uma matriz é ortogonal se, e somente se, for quadrada e invertível tipo A-1 = AT em que AAT = ATA = I.
MATRIZES COMPLEXAS
Este é um exemplo de Matriz Complexa.
Dentro das Matrizes Complexas temos:
*· * As Hermitianas: Se AH = A
* *Anti-hermitianas: Se AH = - A
* Unitárias: Se AH = A-1 e suas linhas (colunas) formam um conjunto ortogonal de vetores ao produto interno de vetores complexos.
· * Normais: Uma Matriz quadrada é Normal se AAH = AHA
APLICAÇÕES DAS MATRIZES
Certamente o ramo mais prodigioso do campo das Matrizes é o computacional em que o uso de vetores e operações matriciais é indispensável, seja na elaboração e desenvolvimento de softwares às imagens geradas de filmes e fotos. Cada filme ou foto carrega uma quantidade incrível de pixels, que são calculadas por matrizes e que, por sua vez, são mais bem transportadas por matrizes linhas ou colunas (vetores). Para a obtenção de rotações em computação gráfica, às grandezas geradas por escalares e tensores na mecânica, nos circuitos elétricos e suas fiações e linhas bem como na distribuição de energia elétrica, nas comunicações, redes de transportes e etc. Não obstante elas também têm aplicabilidade na vida pratica, não sendo necessariamente apenas nas ciências aplicadas.
No artigo de Cristiani dos Santos Campos, (SANTOS, 2008, p.19-20), uma professora de Jandaia do Sul, Paraná, ela faz um comparativo entre os gastos calóricos com a alimentação intermediada por exercícios físicos. Baseando os dados numa pessoa de 60 kg de peso corporal em atividades físicas de tempo de 1 hora, montou uma tabela, como a que se segue:
Durante uma semana em acompanhamento de uma hora, teríamos
Das duas Matrizes é possível construir uma associação de Matrizes e determinar a quantidade de calorias gasta por dia por essa pessoa, assim:
Daí é possível concluir que seguindo a dieta de alimentação e exercícios físicos, na segunda – feira a pessoa gastará 552 calorias, na terça-feira, 890 calorias, na quarta-feira 1016 calorias, na quinta-feira 895 calorias e na sexta-feira 678 calorias.
Nesse mesmo estudo a Professora não só mostra as aplicações matriciais no cotidiano, mas como também insere a interdisciplinaridade uma vez que tal estudo foi embasado nos casos de diabetes.
Uma fácil aplicabilidade das Matrizes consiste no estudo das Equações Lineares. Considere um jornal de grande circulação nas cidades do interior nordestino do país. Dessas, tiremos cinco: Petrolina, Juazeiro, Sobradinho, Curaçá e Santa Maria. A tabela a seguir mostra à quantidade vendida desse jornal de segunda a sexta nessas cidades:
Vendas por dia da semana de Segunda a Sexta

Deseja-se saber o preço vendido em cada cidade, durante a semana de segunda a sexta, sabendo o jornal apurou R$ 100.000,00 durante a referida semana.
As duas tabelas apresentadas podem ser escritas em forma de Matrizes. Aqui a Matriz Quantidade, representada por Q e a Matriz Preços, representada por P. Assim temos:
Verificamos que o número de colunas de Q é o mesmo que o número de linhas de P, o que nos permite uma multiplicação, Q.P = F, onde F é a Matriz Faturamento. Fica:
Então em Petrolina e Juazeiro o Jornal custa R$ 1,58, em Sobradinho R$ 3,16 e em Santa Maria e Curaçá, R$ 4,08.



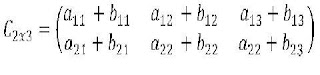




































22 comentários:
Um bom texto de aplicação de Matrizes
ótima explicação, adoreei !
ótima explicação Adoorei !
Muito bom o texto, usei para preparar um trabalho.
Texto didático e de boa qualidade teórica. Interessante para quem quer se iniciar no estudo das matrizes.Faltou uma abordagem das matrizes no estudo das cônicas. Mesmo assim gostei bastante.
Parabéns, muito bom!
Transformar uma tabela comum em uma matriz não trás consigo utilidade nenhuma. Na verdade, torna o cálculo desejado muito mais complexo do que o normal. Não que eu não tenha nenhuma familiaridade com a matemática, mas não entendi o exposto acima. Note que a matemática define uma matriz como um conjunto de número e não tabelas de qualquer assunto cotidiano. Lemnbre-se ainda: temos o IMPA - Instituto de Matemática Pura e Aplicada, isto é: temos matemática pura e não aplicada. É o caso de matrizes. Pelo menos não aplicável a nível de ensino médio. Querer forçar todo o conteúdo de matemática a ser aplicado no cotidiano dos alunos é um enorme ERROOOOOO. Está fazendo coisa comuns do dia a dia parecerem mais complicados ainda do que já parecem. Sinto muito por este MODISMO.
Olá pessoal! Obrigado a todos pelos comentários Voltem sempre!!!
Luiz Sergio Oliveira, você está certíssimo. Há muita coisa dentro da Matemática Básica que é muito desnecessário. Necessitamos de revisar os Conteúdos e te digo que isso já está acontecendo. A SBM e a SBEM estão untas, num encontro mitológico a fim de convergirem em ideias efetivas para a escolha dos novos conteúdos para o Ensino Básico que visem tapar lacunas dos atuais. Também me perdoe pela forma como escrevi o post sobre Matrizes, não alcancei o objetivo com você que era a compreensão. Vou melhorar, obrigado!
Agora Luiz, a Matemática é mais do que um Conjunto sobre Números, é um conjunto de ideias lógicas a partir de axiomas, isso dito grosseiramente já que definir matemática é como tentar definir arte. Sobre o IMPA, nossa! Só elogios! É a nossa pérola Luiz, a única estrela acadêmica que insiste em brilhar com peso igual ou maior que muitas constelações internacionais e em meio a escuridão do conhecimento matemático em nosso país!!!
O IMPA trabalha com matemática aplicada sim e se pode notar isso através dos cursos que tem
Ademais, muito dos progressos tecnológicos conquistados pela humanidade, para não dizer todos e cair na besteira das generalizações, se devem a descobertas matemáticas das quais, muitas vezes, não tinha significado prático algum na época de suas descobertas. A exemplo disso a Teoria dos Números Primos, base de uma das mais seguras formas de proteção virtual existente hoje em dia - o RSA.
Em tese o que se tenta buscar estudando matemática é o conhecimento. Sabemos que cedo ou tarde alguém ou alguma coisa precisará dela. Quanto as Matrizes, nossa!!! Ela é muito aplicada, mas mais no nível superior, é bem verdade. Imagina a lógica das linhas e colunas dessa página de internet que estamos nos comunicando: Não seria possível sem o esquema de vetores, que devem a Teoria das Matrizes e Determinantes.
No mais, muito obrigado pela Crítica construtiva e seja sempre bem vindo com suas ideias.
A todos os demais que aqui se expressaram, inclusive você, Luiz, ME PERDOEM PELA DEMORA EM ATUALIZAR a página e o artigo. Estive muuuuuito ocupado e sem tempo, sem mencionar que é difícil escrever símbolos matemáticos aqui sem usar figura, dá um trabalho danado!
A todos meu muito obrigado!
Ótimo texto, matriz é a base p/ a criançada despertar o interesse por criar o treinamento de redes neurais artificiais.
Queridos, boa noite. fico muito triste quando vejo a desinformação se multiplicar. Não é o único artigo que coloca que as matrizes fazem parte, por exemplo, da engenharia. Há uma forçação de barra para se identificar as planilhas usuais do dia a dia com as matrizes. Isto é um verdadeiro absurdo. Na verdade, banco de dados não tem nada a ver com matriz. Absolutamente nada. Fala-se no seu emprego na engenharia civil (na qual milito a mais de trinta anos) criminosamente. As matrizes terão seu lugar APENAS para quem for estudar matemática avançada (Cálculo vetorial mais especificamente) quando se fará sua identificação com vetores (pasmem, matrizes e vetores são a mesma coisa!!!) mas isso para quem for seguir a área tecnológica. Portanto, os futuros médicos, advogados....jamais verão matrizes na vida, senão disfarçadas em fenômenos da natureza de caráter vetorial (gravidade, velocidade etc). Finalizando, não se iluda quando você for tirar seu extrato bancário...aquilo não é uma matriz e você não obterá seu saldo achando o determinante do extrato. Um abraço. Fernando Hora.
Em tempo: Resolver sistemas lineares com o teorema de Cramer (usando as matrizes) é da mais extrema elegância.
Olá Fernando Hora, tudo bem?
Desculpa a imensa demora em ver seu comentário, é que tem bastante tempo que não alimento mais a página. Coisas da correria do dia a dia.
Fernando, eu não disse que as Matrizes fazem parte da Engenharia, eu disse que hoje é inconcebível a ideia de estudar engenharia sem falar de matrizes, está lá na emente de quase qualquer curso de engenharia, disse quase porque não é muito legal generalizar.
Ademais, entendo que um engenheiro que queira criar coisas, pode ser que em algum momento ele se depare com algum sistema que envolva matrizes ou algo relacionando, tipo vetores, e precise de alguma teoria aliada a prática para se desenvolver a sua ideia.
Sobre o caso de sua aplicabilidade na Engenharia Civil, da qual você (posso te chamar assim?) parece entender muito bem, não tenho a sua mesma bagagem, mas é certo que estudam álgebra lá, não estudam? A aplicação dela vai muito além do que é ensinado ao jovem engenheiro e depende muito da imaginação e criatividade da pessoa. Vai que ele desenvolva algo que use o estudo de matrizes? Nunca se sabe, né! Mas o que eu disse não foi nem em relação a isso, e sim que estudam elas lá no curso,logo nos primeiros semestres. Se eu estiver errado, desculpa.
Gostaria de saber mais a respeito do que realmente é fundamental na grade de um engenheiro, em especial ao Civil, assim poderei escrever artigos mais precisos e corretos no futuro.
Atenciosamente:
Edmarcos Martins Jordão
Boa noite! Sou professor do ensino médio e gostaria de parabenizar o criador do blog, gostei muito, os exemplos sitados foram de grande valia. Obrigado por dedicar seu tempo a ajudar a disseminar novas idéias e aplicações de matrizes. Continue, pessoas como você que ajudam no momento de diversos apertos.
Até que enfim, alguém com a mesma visão que eu, enquanto ensino da matemática na escola.
Até que enfim, alguém com a mesma visão que eu, enquanto ensino da matemática na escola.
Àqueles que criticam o artigo ora postado: vocês simplesmente não entenderam a intenção do autor, eis que este se propôs a demonstrar possíveis aplicações das matrizes em situações cotidianas (mesmo que impráticas, frente a outros métodos mais eficientes) na medida em que pouquíssimas pessoas imaginam que as matrizes possam ter qualquer outra aplicabilidade além de cair nos vestibulares.
Ainda bem que não estou maluco e existem pessoas que partilham de mesma lucidez.
Ainda bem que não estou maluco e existem pessoas que partilham de mesma lucidez.
Nota 10 para o autor , que resumiu tudo que um aluno de exatas precisa saber para iniciar seu caminho, a forma de utilização no cotidiano é realmente um pouco dificil de se encontrar, mas em setores computacionais empresariais , isso acontece todo o instante....Parabéns pela postagem....!!!
Engenharia_abc....
Bom trabalho. Parabéns!
Excelente trabalho.
Creio que no exemplo dos jornais, o valor da 2. coluna é 4935.a e não 5.579.a
Foi a única divergência.
Grato pelo bom exemplo.
Postar um comentário